题目内容
12.设f(x)=$\left\{\begin{array}{l}{x,x<a}\\{{x}^{2},x≥a}\end{array}\right.$对任意实数b,关于x的方程f(x)-b=0总有实数根,则a的取值范围是[0,1].分析 若对任意实数b,关于x的方程f(x)-b=0总有实数根,即对任意实数b,函数f(x)的图象与直线y=b总有交点,即函数f(x)的值域为R,结合二次函数和一次函数的图象和性质,可得a的取值范围.
解答 解:若对任意实数b,关于x的方程f(x)-b=0总有实数根,
即对任意实数b,函数f(x)的图象与直线y=b总有交点,
即函数f(x)的值域为R,
∵f(x)=$\left\{\begin{array}{l}{x,x<a}\\{{x}^{2},x≥a}\end{array}\right.$,
在同一坐标系中画出y=x与y=x2的图象,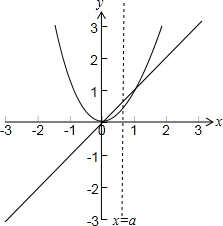
由图可得:当a∈[0,1]时,函数f(x)的值域为R,
故a的取值范围是[0,1],
故答案为:[0,1].
点评 本题考查的知识点是分段函数的应用,函数的图象和性质,其中分析出已知条件等价于函数f(x)的值域为R,是解答的关键.

练习册系列答案
相关题目
3.若函数f(x)在(0,1)内有一个零点,要使零点的近似值的精确度为0.01,则需对区间(0,1)至多二等分( )
| A. | 5次 | B. | 6次 | C. | 7次 | D. | 8次 |
7.若一个几何体的正视图,侧视图和俯视图形状相同,大小均相等,那么这个几何体不可以是( )
| A. | 球 | B. | 三棱锥 | C. | 正方体 | D. | 圆柱 |
2.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线都与圆(x-c)2+y2=ac(c=$\sqrt{{a}^{2}+{b}^{2}}$相切,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2 | D. | $\frac{1+\sqrt{5}}{2}$ |
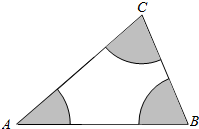 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.