题目内容

14．设an=$\frac{1}{n}$sin$\frac{nπ}{20}$，sn=a1+a2+…+an，在S1，S2，…，S80中，正数的个数是（　　）
A．20B．40C．60D．80

分析 由于f（n）=sin$\frac{nπ}{20}$的周期T=40，由正弦函数性质可知，a1，a2，…，a19＞0，a20=0，a21，a22，…，a39＜0，a40=0，但是f（n）=$\frac{1}{n}$单调递减，a21，…，a39都为负数，但是|a21|＜a1，|a22|＜a2，…，|a39|＜a19，从而可判断．

解答 解：由于f（n）=sin$\frac{nπ}{20}$的周期T=40，
由正弦函数性质可知，a1，a2，…，a19＞0，a20=0，a21，a22，…，a39＜0，a40=0，
且sin$\frac{21π}{20}$=-sin$\frac{π}{20}$，sin$\frac{22π}{20}$=-sin$\frac{2π}{20}$，…但是f（n）=$\frac{1}{n}$单调递减，
a21，…，a39都为负数，但是|a21|＜a1，|a22|＜a2，…，|a39|＜a19，
∴S1，S2，…，S20中都为正，而S21，S22，…，S40都为正，
同理S1，S2，…，s60都为正，S1，S2，…，s60，…，s80都为正，
故选D．

点评 本题主要考查了三角函数的周期的应用，数列求和的应用，解题的关键是正弦函数性质的灵活应用．

练习册系列答案
相关题目
4．已知△ABC的内角A，C满足$\frac{sinC}{sinA}$=cos（A+C），则tanC的最大值为$\frac{\sqrt{2}}{4}$．
5．已知变量x，y满足条件$\left\{\begin{array}{l}{y≤2x}\\{x+y≤m}\\{y≥-1}\end{array}\right.$，若z=y-x的最小值为-3，则z=y-x的最大值为$\frac{1}{3}$．
2．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两条渐近线都与圆（x-c）2+y2=ac（c=$\sqrt{{a}^{2}+{b}^{2}}$相切，则双曲线的离心率为（　　）
A．$\frac{\sqrt{5}-1}{2}$B．$\frac{\sqrt{5}}{2}$C．2D．$\frac{1+\sqrt{5}}{2}$
9．已知函数f（x）=$\left\{\begin{array}{l}{-{e}^{2x}+bx+c，}&{x≤1}\\{a（{x}^{2}lnx-x+1）+1，}&{x≥1}\end{array}\right.$
（Ⅰ）若0＜b＜2e2，试讨论函数f（x）在区间（-∞，1]上的单调性；
（Ⅱ）若函数f（x）在x=0处取得极值1，求f（x）在区间[-2，2]上的最大值．
19．设m＞1，在线性约束条件$\left\{\begin{array}{l}{y≥x}\\{y≤mx}\\{x+y≤1}\end{array}\right.$下，目标函数z=x+5y的最大值为4，则m的值为3．此时，约束条件下的平面区域的面积为$\frac{1}{8}$．
6．某几何体的三视图如图所示，则该几何体的体积为（　　）
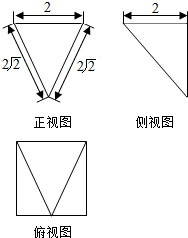
A．$\frac{4\sqrt{6}}{3}$B．2$\sqrt{6}$C．$\frac{4\sqrt{7}}{3}$D．4$\sqrt{7}$
3．如图，已知三棱锥O-ABC的三条侧棱OA，OB，OC两两垂直，且OA=OC=4，OB=3．
（1）求O点到平面ABC的距离；
（2）设A1、B1、C1依次为线段OA，OB，OC内的点，证明：△A1B1C1是锐角三角形．
4．在一台车床上生产某种零件，此零件的月产量与零件的市场价格具有随机性，且互不影响，其具体情况如表：
表1：零件某年的每月产量（个/月）
月份第一季度第二季度第三季度第四季度
123456789101112
产量500400625625500500500500500400400625
表2：零件市场价格（元/个）
零件市场价格810
概率0.40.6
（Ⅰ） 请你根据表1中所给的数据，判断该零件哪个季度的月产量方差最大；（结论不要求证明）
（Ⅱ） 随机抽取该种零件的一个月的月产量记为X，求X的分布列；
（Ⅲ）随机抽取该种零件的一个月的月产量，设Y表示该种零件的月产值，求Y的分布列及期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网