题目内容
9.若点(1,-2)与点(-2,0)在直线x+y+a=0的两侧,同时点(1,-2)和点(-1,-4)都在不等式bx+y+2<0所表示的区域内,求a+b与a-b的取值范围.分析 根据二元一次不等式表示平面区域,求出a,b的取值范围,结合不等式的性质进行求解即可.
解答 解:若点(1,-2)与点(-2,0)在直线x+y+a=0的两侧,则(1-2+a)(-2+a)<0,
即(a-1)(a-2)<0,解得1<a<2,
点(1,-2)和点(-1,-4)都在不等式bx+y+2<0所表示的区域内,
则b-2+2<0且-b-4+2<0,
即b<0,且b>-2,
即-2<b<0,
则-1<a+b<2,
0<-b<2,
1<a-b<4,
即a+b与a-b的取值范围分别是(-1,2),(1,4).
点评 本题主要考查不等式性质的应用,根据点与直线的位置关系求出a,b的取值范围是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.记方程①:x2+a1x+1=0,方程②:x2+a2x+2=0,方程③:x2+a3x+4=0,其中a1,a2,a3是正实数.当a1,a2,a3成等比数列时,下列选项中,能推出方程③无实根的是( )
| A. | 方程①有实根,且②有实根 | B. | 方程①有实根,且②无实根 | ||
| C. | 方程①无实根,且②有实根 | D. | 方程①无实根,且②无实根 |
18.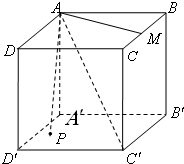 如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
 如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )| A. | 一段圆弧 | B. | 一段椭圆弧 | C. | 一段双曲线弧 | D. | 一段抛物线弧 |
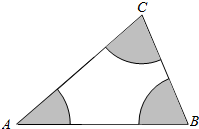 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.