题目内容
【题目】已知![]() 的圆心为
的圆心为![]() ,
,![]() 的圆心为
的圆心为![]() ,一动圆与圆
,一动圆与圆![]() 内切,与圆
内切,与圆![]() 外切.
外切.
(1)求动圆圆心的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,交直线
两点,交直线![]() 于点
于点![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1) ![]() ;(2) 存在,2.
;(2) 存在,2.
【解析】
(1)利用动圆与圆![]() 内切,与圆
内切,与圆![]() 外切可得动圆圆心满足的几何性质,再根据椭圆的定义可得
外切可得动圆圆心满足的几何性质,再根据椭圆的定义可得![]() 的轨迹方程.
的轨迹方程.
(2)设![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,则
,则![]() ,联立直线方程和椭圆方程,消去
,联立直线方程和椭圆方程,消去![]() 后利用韦达定理化简前者可得
后利用韦达定理化简前者可得![]() 的值.
的值.

(1)设动圆圆心![]() ,设动圆的半径为
,设动圆的半径为![]() ,由题意有
,由题意有
![]() ,
,![]() ,消
,消![]() 得到:
得到:![]() ,
,
故轨迹![]() 的方程为:
的方程为:![]() ,它是椭圆.
,它是椭圆.
(2)由己知得![]() ,由题知直线
,由题知直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
![]() 等价于
等价于![]() 即
即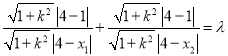 ,
,
即证明![]() 成立,
成立,
也即![]() ①.
①.
联立方程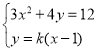 ,消去
,消去![]() 得:
得:
![]()
由韦达定理得![]() ,
,![]()
代入①可得
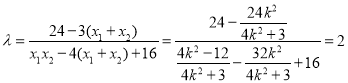
所以存在实数![]() 满足题意.
满足题意.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】某校实行选科走班制度,张毅同学的选择是地理、生物、政治这三科,且生物在![]() 层班级.该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法的种数为( )
层班级.该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法的种数为( )
第一节 | 第二节 | 第三节 | 第四节 |
地理1班 | 化学 | 地理2班 | 化学 |
生物 | 化学 | 生物 | 历史 |
物理 | 生物 | 物理 | 生物 |
物理 | 生物 | 物理 | 物理 |
政治1班 | 物理A层3班 | 政治2班 | 政治3班 |
A. 4B. 5C. 6D. 7