题目内容
【题目】
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4.现从盒子中随机抽取卡片.
(1)若一次抽取3张卡片,求3张卡片上数字之和大于7的概率;
(2)若第一次抽1张卡片,放回后再抽取1张卡片,求两次抽取中至少一次抽到数字3的概率.
【答案】(1)0.5(2)![]()
【解析】
试题(1)由题意知本题是一个古典概型,试验包含的所有事件是任取三张卡片,三张卡片上的数字全部可能的结果,可以列举出,而满足条件得事件数字之和大于7的,可以从列举出的结果中看出;(2)列举出每次抽1张,连续抽取两张全部可能的基本结果,而满足条件的事件是两次抽取中至少一次抽到数字3,从前面列举出的结果中找出来.
试题解析:(1)由题意知本题是一个古典概型,设A表示事件“抽取3张卡片上的数字之和大于7”,
∵ 任取三张卡片,三张卡片上的数字全部可能的结果是{1、2、3},{1、2、4},{1、3、4},{2、3、4}共4个,其中数字之和大于7的是{1、3、4},{2、3、4},
∴P(A)=0.5
(2)设B表示事件“至少一次抽到3”,
∵每次抽1张,连续抽取两张全部可能的基本结果有:(1、1)(1、2)(1、3)(1、4)(2、1)(2、2)(2、3)(2、4)(3、1)(3、2)(3、3)(3、4)(4、1)(4、2)(4、3)(4、4),共16个.
事件B包含的基本结果有(1、3)(2、3)(3、1)(3、2)(3、3)(3、4)(4、3),共7个基本结果.
∴所求事件的概率为P(B)= ![]()

【题目】(请写出式子在写计算结果)有4个不同的小球,4个不同的盒子,现在要把球全部放入盒内:
(1)共有多少种方法?
(2)若每个盒子不空,共有多少种不同的方法?
(3)恰有一个盒子不放球,共有多少种放法?
【题目】为了解某班学生喜欢打篮球是否与性别有关,对本班50人进行了问卷调查,得到如表的![]() 列联表:
列联表:
喜欢打篮球 | 不喜欢打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中喜欢打篮球的学生为30人.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜欢打篮球与性别有关?请说明你的理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
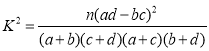 ,其中
,其中![]() .
.


