题目内容

14．在△ABC中，∠A，∠B满足关系式1-tanAtanB＜0，则△ABC是（　　）
A．锐角三角形B．直角三角形C．钝角三角形D．任意三角形

分析 根据A与B的范围以及tanAtanB＞1，得到tanA和tanB都大于0，即可得到A与B都为锐角，然后判断出tanC大于0，得到C为锐角，可得此三角形为锐角三角形．

解答 解：△ABC中，由1-tanAtanB＜0可得tanAtanB＞1，∴tanA＞0，且tanB＞0，
故A、B都是锐角，∴-tanC=tan（A+B）=$\frac{tanA+tanB}{1-tanAtanB}$＜0，tanC＞0，即C为锐角，
∴△ABC是锐角三角形，
故选：A．

点评 本题主要考查了三角形的形状判断，用的知识有两角和的正切函数公式、诱导公式，属于基础题．

练习册系列答案
相关题目
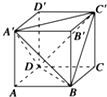4．如图，正方体ABCD-A′B′C′D′的棱长为a，连接A′C′，A′D，A′B，BD，BC′，C′D，得到一个三棱锥，求：
（1）三棱锥A′-BC′D的表面积与正方体表面积的比值；
（2）三棱锥A′-BC′D的体积．
5．已知集合A={2，4，x2-x}，若{6}⊆A，则x=-3或2．
2．函数y=$\sqrt{1-|x-2|}$+$\frac{1}{\root{3}{2x-5}}$的定义域为{x|1≤x≤3且x≠$\frac{5}{2}$}．
9．求棱长为8的正三棱锥的表面积和体积．
19．已知函数f（x）满足f（x）•f（x+2）=13．
（1）求证：f（x）是周期函数；
（2）若f（1）=2，求f（99）的值；
（3）若当x∈[0，2]时，f（x）=x，试求x∈[4，8]时函数f（x）的解析式．
6．正八边形对角线的条数为（　　）
A．156B．48C．28D．20
3．计算：（$\frac{i}{1+i}$）2+（$\frac{i}{1-i}$）2．
8．设x，y满足约束条件$\left\{\begin{array}{l}3x-y-2≤0\\ x-y≥0\\ x≥0，y≥0\end{array}\right.$，若目标函数z=ax+by（a＞0，b＞0）的最大值为2，则$\frac{1}{a}+\frac{1}{b}$的最小值为2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网