题目内容
8.设x,y满足约束条件$\left\{\begin{array}{l}3x-y-2≤0\\ x-y≥0\\ x≥0,y≥0\end{array}\right.$,若目标函数z=ax+by(a>0,b>0)的最大值为2,则$\frac{1}{a}+\frac{1}{b}$的最小值为2.分析 作出题中不等式组表示的平面区域,得如图的△AB0及其内部,再将目标函数z=ax+by对应的直线进行平移,可得当x=1且y=1时,z最大值=a+b=2.由此再利用基本不等式求最值,可得$\frac{1}{a}+\frac{1}{b}$的最小值.
解答 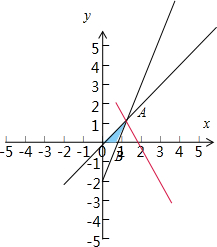 解:作出不等式组$\left\{\begin{array}{l}3x-y-2≤0\\ x-y≥0\\ x≥0,y≥0\end{array}\right.$表示的平面区域,
解:作出不等式组$\left\{\begin{array}{l}3x-y-2≤0\\ x-y≥0\\ x≥0,y≥0\end{array}\right.$表示的平面区域,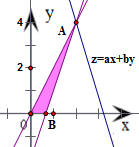
得到如图的△ABO及其内部,$\left\{\begin{array}{l}3x-y-2=0\\ x-y=0\end{array}\right.$其中A(1,1),
B($\frac{2}{3}$,0),0为坐标原点
设z=F(x,y)=ax+by,将直线l:z=ax+by进行平移,
由a>0且b>0得直线l的斜率为负数,观察y轴上的截距变化,可得当l经过点A时,目标函数z达到最大值
∴z最大值=F(1,1)=a+b=2,
因此,$\frac{1}{a}+\frac{1}{b}$=$\frac{1}{2}$(a+b)($\frac{1}{a}+\frac{1}{b}$)=$\frac{1}{2}$(2+$\frac{b}{a}+\frac{a}{b}$)
∵a>0且b>0,$\frac{b}{a}+\frac{a}{b}≥2$,∴$\frac{1}{a}+\frac{1}{b}$≥2,
当且仅当a=b=1时,等号成立
∴$\frac{1}{a}+\frac{1}{b}$的最小值为:2.
故答案为:2
点评 本题给出二元一次不等式组,求在已知目标函数的最大值为1的情况下求$\frac{1}{a}+\frac{1}{b}$的最小值,着重考查了基本不等式、二元一次不等式组表示的平面区域和简单的线性规划等知识,属于中档题.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 任意三角形 |

| A. | 4$\sqrt{3}$π | B. | $\frac{4\sqrt{3}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{4\sqrt{2}π}{3}$ |
| A. | $\frac{lnx+1}{{x}^{2}}$ | B. | $\frac{lnx-1}{{x}^{2}}$ | C. | $\frac{x+lnx}{{x}^{2}}$ | D. | $\frac{1-lnx}{{x}^{2}}$ |
| A. | 第5项 | B. | 第6项 | C. | 第7项 | D. | 第5项或第6项 |