题目内容
9.求棱长为8的正三棱锥的表面积和体积.分析 由正四面体的棱长为8,所以此四面体一定可以放在棱长为4$\sqrt{2}$的正方体中,所以此四面体的外接球即为此正方体的外接球,由此能求出此四面体的外接球的半径,再代入面积公式、体积公式计算.
解答 解:∵正四面体的棱长为8,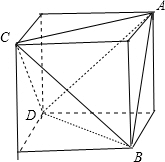
∴此四面体一定可以放在正方体中,
∴我们可以在正方体中寻找此四面体.
如图所示,四面体ABCD满足题意,BC=8,
∴正方体的棱长为4$\sqrt{2}$,
∴此四面体的外接球即为此正方体的外接球,
∵外接球的直径=正方体的对角线长,
∴外接球的半径为R=$\frac{1}{2}$×$\sqrt{3}$×4$\sqrt{2}$=2$\sqrt{6}$,
∴球的表面积S=4π•24=96π;
球的体积为V=$\frac{4}{3}π•(2\sqrt{6})^{3}$=64$\sqrt{6}$π.
点评 本题考查几何体的接体问题,考查了空间想象能力,其解答的关键是根据几何体的结构特征,求出接体几何元素的数据,代入面积、体积公式分别求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在△ABC中,∠A,∠B满足关系式1-tanAtanB<0,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 任意三角形 |
18.函数y=$\frac{1}{1-\sqrt{x}}$+$\frac{1}{1+\sqrt{x}}$的导数y′=( )
| A. | $\frac{4x}{(1-x)^{2}}$ | B. | -$\frac{4x}{(1-x)^{2}}$ | C. | $\frac{2}{(1-x)^{2}}$ | D. | -$\frac{2}{(1-x)^{2}}$ |