题目内容
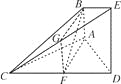
【题目】在如图所示的几何体中，AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD＝DE＝2AB，F为CD的中点．
(1)求证：AF∥平面BCE；
(2)求证：平面BCE⊥平面CDE.
【答案】（1）见解析 （2）见解析
【解析】
试题证明：(1)如图，取CE的中点G，连接FG，BG.
∵F为CD的中点，∴GF∥DE，且GF＝
DE.
∵AB⊥平面ACD，DE⊥平面ACD，∴AB∥DE.∴GF∥AB.
又AB＝DE，∴GF＝AB.∴四边形GFAB为平行四边形，则AF∥BG.
∵AF平面BCE，BG平面BCE，∴AF∥平面BCE.
(2)∵△ACD为等边三角形，F为CD的中点，∴AF⊥CD.
∵DE⊥平面ACD，AF平面ACD，∴DE⊥AF.又CD∩DE＝D，∴AF⊥平面CDE.
∵BG∥AF，∴BG⊥平面CDE.∵BG平面BCE，∴平面BCE⊥平面CDE.
【题目】某大型单位举行了一次全体员工都参加的考试，从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数（以十位数字为茎，个位数字为叶）：
若分数不低于95分，则称该员工的成绩为“优秀”.
（1）从这20人中任取3人，求恰有1人成绩“优秀”的概率；
（2）根据这20人的分数补全下方的频率分布表和频率分布直方图，并根据频率分布直方图解决下面的问题.
组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
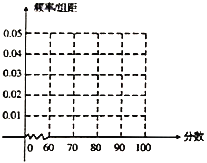
①估计所有员工的平均分数（同一组中的数据用该组区间的中点值作代表）；
②若从所有员工中任选3人，记
表示抽到的员工成绩为“优秀”的人数，求
的分布列和数学期望.
【题目】某保险公司有一款保险产品的历史收益率（收益率
利润
保费收入）的频率分布直方图如图所示：
（1）试估计这款保险产品的收益率的平均值；
（2）设每份保单的保费在20元的基础上每增加
元，对应的销量为
（万份）．从历史销售记录中抽样得到如下5组
与
的对应数据：
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表，知
与
有较强的线性相关关系，且据此计算出的回归方程为
．
（ⅰ）求参数
的值；
（ⅱ）若把回归方程
当作
与
的线性关系，用（1）中求出的收益率的平均值作为此产品的收益率，试问每份保单的保费定为多少元时此产品可获得最大利润，并求出最大利润．注：保险产品的保费收入
每份保单的保费
销量．
