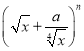题目内容
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):

若分数不低于95分,则称该员工的成绩为“优秀”.
(1)从这20人中任取3人,求恰有1人成绩“优秀”的概率;
(2)根据这20人的分数补全下方的频率分布表和频率分布直方图,并根据频率分布直方图解决下面的问题.
组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
①估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表);
②若从所有员工中任选3人,记![]() 表示抽到的员工成绩为“优秀”的人数,求
表示抽到的员工成绩为“优秀”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ;(2)①82,②分布列见解析,
;(2)①82,②分布列见解析,![]()
【解析】
(1)从20人中任取3人共有![]() 种结果,恰有1人成绩“优秀”共有
种结果,恰有1人成绩“优秀”共有![]() 种结果,利用古典概型的概率计算公式计算即可;
种结果,利用古典概型的概率计算公式计算即可;
(2)①平均数的估计值为各小矩形的组中值与其面积乘积的和;②要注意![]() 服从的是二项分布,不是超几何分布,利用二项分布的分布列及期望公式求解即可.
服从的是二项分布,不是超几何分布,利用二项分布的分布列及期望公式求解即可.
(1)设从20人中任取3人恰有1人成绩“优秀”为事件![]() ,
,
则![]() ,所以,恰有1人“优秀”的概率为
,所以,恰有1人“优秀”的概率为![]() .
.
(2)
组别 | 分组 | 频数 | 频率 |
|
1 |
| 2 |
| 0.01 |
2 |
| 6 |
| 0.03 |
3 |
| 8 |
| 0.04 |
4 |
| 4 |
| 0.02 |
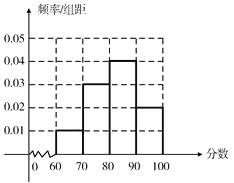
①![]() ,
,
估计所有员工的平均分为82
②![]() 的可能取值为0、1、2、3,随机选取1人是“优秀”的概率为
的可能取值为0、1、2、3,随机选取1人是“优秀”的概率为![]() ,
,
∴![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
∴![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∵![]() ,∴数学期望
,∴数学期望![]() .
.

【题目】(本小题满分12分)为预防H1N1病毒爆发,某生物技术公司研制出一种新流感
疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司
选定2000个流感样本分成三组,测试结果如下表:
分组 | A组 | B组 | C组 |
疫苗有效 | 673 |
|
|
疫苗无效 | 77 | 90 |
|
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(I)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取样本多少个?
(II)已知![]() ,
,![]() ,求通过测试的概率.
,求通过测试的概率.