题目内容
【题目】已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点,且
上的动点,且![]() ,设
,设![]() (
(![]() ),沿
),沿![]() 将梯形
将梯形![]() 翻折,使平面
翻折,使平面![]() 平面
平面![]() ,如图.
,如图.

(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为![]() ,求
,求![]() 的最大值;
的最大值;
(3)当![]() 取得最大值时,求二面角
取得最大值时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)如图所示:![]() 于
于![]() ,连接
,连接![]() ,证明
,证明![]() ,
,![]() 得到
得到![]() 平面
平面![]() ,得到证明.
,得到证明.
(2)计算得到![]() ,根据二次函数性质得到答案.
,根据二次函数性质得到答案.
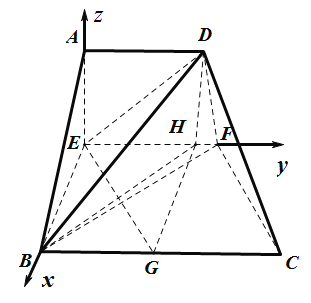
(3)如图所示:以![]() 为
为![]() 轴建立空间直角坐标系,平面
轴建立空间直角坐标系,平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,计算向量夹角得到答案.
,计算向量夹角得到答案.
(1)如图所示:![]() 于
于![]() ,连接
,连接![]() ,
,
平面![]() 平面
平面![]() ,
,![]() ,故
,故![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() ,易知
,易知![]() 为正方形,故
为正方形,故![]() ,
,![]() ,
,
故![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() .
.
(2)![]() ,
,
故![]() .
.
(3)如图所示:以![]() 为
为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
易知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则 ,即
,即![]() ,
,
取![]() ,得到
,得到![]() ,故
,故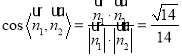 ,
,
观察知二面角![]() 的平面角为钝角,故余弦值为
的平面角为钝角,故余弦值为![]() .
.

练习册系列答案
相关题目
【题目】某大型企业针对改善员工福利的![]() ,
,![]() ,
,![]() 三种方案进行了问卷调查,调查结果如下:
三种方案进行了问卷调查,调查结果如下:
支持 | 支持 | 支持 | |
35岁以下的人数 | 200 | 400 | 800 |
35岁及以上的人数 | 100 | 100 | 400 |
(1)从所有参与调查的人中,用分层随机抽样的方法抽取![]() 人,已知从支持
人,已知从支持![]() 方案的人中抽取了6人,求
方案的人中抽取了6人,求![]() 的值.
的值.
(2)从支持![]() 方案的人中,用分层随机抽样的方法抽取5人,这5人中年龄在35岁及以上的人数是多少?年龄在35岁以下的人数是多少?
方案的人中,用分层随机抽样的方法抽取5人,这5人中年龄在35岁及以上的人数是多少?年龄在35岁以下的人数是多少?
