题目内容
14．
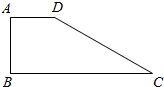如图所示．已知直角梯形ABCD，BC∥AD，∠ABC=90°AB=5cm，BC=16cm，AD=4cm，求以AB所在直线为轴旋转一周所得几何体的表面积．
分析 根据题意知由直角梯形绕其直腰所得的几何体是圆台，根据题意求出圆台的两底面的半径和母线长，再代入表面积公式求解．
解答 解：由题意知，将此梯形以AB所在直线为轴旋转一周，所得几何体是圆台，
则圆台的上底圆的半径是4cm，下底圆的半径是16cm，高是5cm，
则母线长是13cm，
∴此圆台的表面积是16π+256π+π（4+16）×13=532πcm2．
点评 本题的考点是旋转体的表面积的求法，关键是由平面图形想象出所得旋转体的结构特征，再求出所得旋转体的高以及其它几何元素的长度，考查了空间想象能力．
练习册系列答案
相关题目
4．
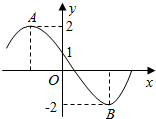函数f（x）=2sin（ωx+φ）的部分图象如图所示，其中A，B两点之间的距离为5，那么下列说法正确的是（ ）
函数f（x）=2sin（ωx+φ）的部分图象如图所示，其中A，B两点之间的距离为5，那么下列说法正确的是（ ）| A． | 函数f（x）的最小正周期为8 | |
| B． | f（3）=-$\frac{1}{2}$ | |
| C． | x=$\frac{3}{2}$是函数f（x）的一条对称轴 | |
| D． | 函数f（x）向右平移一个单位长度后所得的函数为偶函数 |
4．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1有相同的长轴，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长与椭圆$\frac{{y}^{2}}{21}$+$\frac{{x}^{2}}{9}$=1的短轴长相等，则（ ）
| A． | a2=25，b2=16 | B． | a2=9，b2=25 | ||
| C． | a2=25，b2=9或a2=9，b2=25 | D． | a2=25，b2=9 |