题目内容
6.已知圆方程为x2-4x+y2-2y-4=0,它与x轴交于A,B两点,求|AB|.分析 通过y=0,求出x的值,即可得到|AB|.
解答 解:圆方程为x2-4x+y2-2y-4=0,它与x轴交于A,B两点,令y=0,可得x2-4x-4=0,
解得x=2±2$\sqrt{2}$,
|AB|=|$2+2\sqrt{2}-2+2\sqrt{2}$|=4$\sqrt{2}$.
点评 本题考查直线与圆的位置关系的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若实数x,y满足不等式组$\left\{\begin{array}{l}{y≤3}\\{3x+7y-24≤0}\\{x+3y-8≥0}\end{array}\right.$,则z=x+2y的最大值是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
15.函数f(x)=-3x+7,g(x)=1g(ax2-4x+a),若?x1∈R,?x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
| A. | [0,2] | B. | [0,2) | C. | (2,+∞) | D. | [2,+∞) |
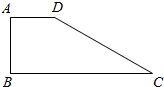 如图所示.已知直角梯形ABCD,BC∥AD,∠ABC=90°AB=5cm,BC=16cm,AD=4cm,求以AB所在直线为轴旋转一周所得几何体的表面积.
如图所示.已知直角梯形ABCD,BC∥AD,∠ABC=90°AB=5cm,BC=16cm,AD=4cm,求以AB所在直线为轴旋转一周所得几何体的表面积.