题目内容
3.已知C1:y=2x-5,C2:x2+y2=k(k>0).当0<k<5时,两曲线有两个交点;当k=5时,两曲线只有一个交点:当k>5时,两曲线没有交点(填k的取值范围)分析 求出圆的圆心到直线的距离与半径比较即可推出结果.
解答 解:圆的圆心(0,0),半径为:$\sqrt{k}$,
圆的圆心到直线的距离为:$\frac{5}{\sqrt{{2}^{2}+({-1)}^{2}}}$=$\sqrt{5}$,
当$\sqrt{k}=\sqrt{5}$即k=5时,直线与圆只有一个交点,
当$\sqrt{k}<\sqrt{5}$即0<k<5时,直线与圆有两个交点,
当$\sqrt{k}>\sqrt{5}$即5<k时,直线与圆没有交点,
故答案为:0<k<5;k=5;k>5.
点评 本题考查直线与圆的位置关系的应用,考查转化思想以及计算能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
8.若实数a,b满足ab-4a-b+1=0(a>1),则(a+1)(b+2)的最小值为( )
| A. | 24 | B. | 25 | C. | 27 | D. | 30 |
15.函数f(x)=-3x+7,g(x)=1g(ax2-4x+a),若?x1∈R,?x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
| A. | [0,2] | B. | [0,2) | C. | (2,+∞) | D. | [2,+∞) |
12.定义在R上的函数y=f(x),满足f(x+2)=-$\frac{1}{f(x)}$,则( )
| A. | f(x)不是周期函数 | B. | f(x)是周期函数,且最小正周期为2 | ||
| C. | f(x)是周期函数,且最小正周期为4 | D. | f(x)是周期函数,且4是它的一个周期 |
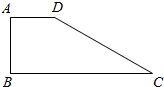 如图所示.已知直角梯形ABCD,BC∥AD,∠ABC=90°AB=5cm,BC=16cm,AD=4cm,求以AB所在直线为轴旋转一周所得几何体的表面积.
如图所示.已知直角梯形ABCD,BC∥AD,∠ABC=90°AB=5cm,BC=16cm,AD=4cm,求以AB所在直线为轴旋转一周所得几何体的表面积.