题目内容
19.若不等式2x2+(1-a)y2≥(3+a)xy(x>0,y>0)恒成立.则实数a的最大值为4$\sqrt{3}$-7.分析 化简不等式可得a≤$\frac{2{x}^{2}-3xy+{y}^{2}}{xy+{y}^{2}}$,令$\frac{2{x}^{2}-3xy+{y}^{2}}{xy+{y}^{2}}$=$\frac{2(\frac{x}{y})^{2}-3\frac{x}{y}+1}{\frac{x}{y}+1}$,再令b=$\frac{x}{y}$>0,则$\frac{2(\frac{x}{y})^{2}-3\frac{x}{y}+1}{\frac{x}{y}+1}$=$\frac{2{b}^{2}-3b+1}{b+1}$,令f(b)=$\frac{2{b}^{2}-3b+1}{b+1}$=2(b+1)+$\frac{6}{b+1}$-7,从而利用基本不等式求最小值,从而解得.
解答 解:∵2x2+(1-a)y2≥(3+a)xy,
∴2x2+y2-3xy≥a(y2+xy),
又∵x>0,y>0,
∴a≤$\frac{2{x}^{2}-3xy+{y}^{2}}{xy+{y}^{2}}$,
令$\frac{2{x}^{2}-3xy+{y}^{2}}{xy+{y}^{2}}$=$\frac{2(\frac{x}{y})^{2}-3\frac{x}{y}+1}{\frac{x}{y}+1}$,
令b=$\frac{x}{y}$>0,则$\frac{2(\frac{x}{y})^{2}-3\frac{x}{y}+1}{\frac{x}{y}+1}$=$\frac{2{b}^{2}-3b+1}{b+1}$,
令f(b)=$\frac{2{b}^{2}-3b+1}{b+1}$=2(b+1)+$\frac{6}{b+1}$-7,
∵2(b+1)+$\frac{6}{b+1}$≥4$\sqrt{3}$,
(当且仅当2(b+1)=$\frac{6}{b+1}$,即b=$\sqrt{3}$-1时,等号成立),
∴2(b+1)+$\frac{6}{b+1}$-7≥4$\sqrt{3}$-7,
∵a≤$\frac{2{x}^{2}-3xy+{y}^{2}}{xy+{y}^{2}}$恒成立,
∴a≤4$\sqrt{3}$-7,
故答案为:4$\sqrt{3}$-7.
点评 本题考查了不等式的化简与恒成立问题的化简与应用,同时考查了函数与不等式的关系应用.

 阅读快车系列答案
阅读快车系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
| A. | $\left.\begin{array}{l}{A∈α}\\{a?α}\end{array}\right\}$⇒A∈α | B. | $\left.\begin{array}{l}{A∈α,A∈β}\\{α∩β=α}\end{array}\right\}$⇒A∈α | ||
| C. | $\left.\begin{array}{l}{A∈α}\\{A∈β}\end{array}\right\}$⇒α∩β=A | D. | $\left.\begin{array}{l}{A∈α}\\{B∈α}\end{array}\right\}$⇒AB?α |
| A. | 24 | B. | 25 | C. | 27 | D. | 30 |
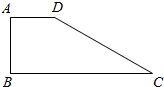 如图所示.已知直角梯形ABCD,BC∥AD,∠ABC=90°AB=5cm,BC=16cm,AD=4cm,求以AB所在直线为轴旋转一周所得几何体的表面积.
如图所示.已知直角梯形ABCD,BC∥AD,∠ABC=90°AB=5cm,BC=16cm,AD=4cm,求以AB所在直线为轴旋转一周所得几何体的表面积.