题目内容
19.在直角坐标系xOy中,以原点O为极点,以x轴正半轴为极轴,圆C的极坐标方程为$ρ=4\sqrt{2}cos(θ+\frac{π}{4})$.(Ⅰ)将圆C的极坐标方程化为直角坐标方程;
(Ⅱ)过点P(2,0)作斜率为1直线l与圆C交于A,B两点,试求$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}$的值.
分析 (Ⅰ)根据直线参数方程的一般式,即可写出,化简圆的极坐标方程,运用ρcosθ=x,ρsinθ=y,即可普通方程;
(Ⅱ)求出过点P(2,0)作斜率为1直线l的参数方程,代入到圆的方程中,得到关于t的方程,运用韦达定理,以及参数t的几何意义,即可求出结果.
解答 解:(Ⅰ)由$ρ=4\sqrt{2}cos(θ+\frac{π}{4})$,可得ρ=4cosθ-4sinθ,∴ρ2=4ρcosθ-4ρsinθ,∴x2+y2=4x-4y,即(x-2)2+(y+2)2=8;
(Ⅱ)过点P(2,0)作斜率为1直线l的参数方程为$\left\{\begin{array}{l}{x=2+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$
代入(x-2)2+(y+2)2=8得t2+2$\sqrt{2}$t-4=0,
A,B对应的参数为t1、t2,则t1+t2=-2$\sqrt{2}$,t1t2=-4,
由t的意义可得$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}$=$\frac{1}{|{t}_{1}|}$+$\frac{1}{|{t}_{2}|}$=$\frac{|{t}_{1}-{t}_{2}|}{|{t}_{1}{t}_{2}|}$=$\frac{\sqrt{6}}{2}$.
点评 本题考查直线的参数方程、以及极坐标方程与普通方程的互化,同时考查直线参数方程的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在某地人们发现某种蟋蟀1min所叫次数与当地气温之间近似为一次函数,下面是蟋蟀所叫次数与气温变化情况对照表:
(1)根据表中数据确定该一次函数的关系式;
(2)如果蟋蟀1min叫了63次,那么该地当时的温度大约为多少摄氏度;
(3)能用所求的函数模型来预测蟋蟀在0℃时所鸣叫的次数.
| 蟋蟀叫次数 | … | 84 | 98 | 119 | … |
| 温度(℃) | … | 15 | 17 | 20 | … |
(2)如果蟋蟀1min叫了63次,那么该地当时的温度大约为多少摄氏度;
(3)能用所求的函数模型来预测蟋蟀在0℃时所鸣叫的次数.
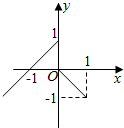 (1)已知y=f(x)的图象如图所示,求f(x);
(1)已知y=f(x)的图象如图所示,求f(x);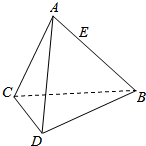 如图,棱长为4的正四面体ABCD,AE=$\frac{1}{3}$AB,试建立适当的坐标系,写出各点的坐标.
如图,棱长为4的正四面体ABCD,AE=$\frac{1}{3}$AB,试建立适当的坐标系,写出各点的坐标.