题目内容
4．
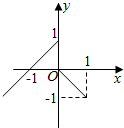（1）已知y=f（x）的图象如图所示，求f（x）；（2）已知f（x+$\frac{1}{x}$）=x2+$\frac{1}{{x}^{2}}$，求f（x）．
分析 （1）分别求出x＜0，0≤x≤1时的函数的表达式即可；（2）通过换元法求出函数的解析式即可．
解答 解：（1）x＜0时，f（x）=x+1，
0≤x≤1时，f（x）=-x，
∴f（x）=$\left\{\begin{array}{l}{x+1，x＜0}\\{-x，0≤x≤1}\end{array}\right.$；
（2）f（x+$\frac{1}{x}$）=x2+$\frac{1}{{x}^{2}}$=${（x+\frac{1}{x}）}^{2}$-2，
令t=x+$\frac{1}{x}$，则t≥2或t≤-2，
∴f（t）=t2-2，
∴f（x）=x2-2，（x≥2或x≤-2）．
点评 本题考查了求一次函数，二次函数的解析式问题，考查数形结合思想，是一道基础题．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
16．若a，b∈R，下面各式总能成立的是（ ）
| A． | （$\root{6}{a}$）6-（$\root{6}{b}$）6=a-b | B． | $\root{8}{（{a}^{2}+{b}^{2}）^{8}}$=a2+b2 | ||
| C． | $\root{4}{{a}^{4}}$-$\root{4}{{b}^{4}}$=a-b | D． | $\root{10}{（a+b）^{10}}$=a+b |