题目内容
公差小于0的等差数列{an}中,且(a3)2=(a9)2,则数列{an}的前n项和Sn取得最大值时的n的值是
| A.6 | B.7 | C.5或6 | D.6或7 |
C
试题分析:根据|a3|=|a9|,可两端平方,得到首项a1与公差d的关系,从而可求得通项公式an,利用
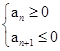 即可求得前n项和Sn取得最大值时的自然数n 的值.
即可求得前n项和Sn取得最大值时的自然数n 的值.根据题意可知
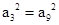 2即(
2即(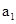 +2d)2=(
+2d)2=(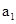 +8d)2,∴
+8d)2,∴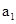 =-5d,∴
=-5d,∴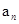 =(n-6)d(d<0),
=(n-6)d(d<0),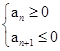 ,则得
,则得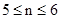
点评:本题考查等差数列的前n项和,着重考查学生将灵活运用等差数列的通项公式解决问题的能力,也可求得Sn关于d的二次函数式,配方解决;属于中档题.

练习册系列答案
相关题目
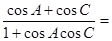 。
。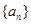 中,
中,  ,通过计算
,通过计算 的值,可猜想出这个数列的通项公式为
的值,可猜想出这个数列的通项公式为
 而言,若
而言,若 是以
是以 为公差的等差数列,
为公差的等差数列,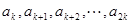 是以
是以 为公差的等差数列,依此类推,我们就称该数列为等差数列接龙,已知
为公差的等差数列,依此类推,我们就称该数列为等差数列接龙,已知 ,则
,则 等于
等于  为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( )
为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( )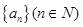 满足
满足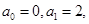 且对一切
且对一切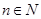 ,有
,有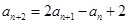
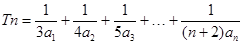 ,求
,求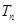 的取值范围.
的取值范围. 中,
中, ,若在每相邻两项间各插入一个数,使之成等差数列,那么新的等差数列的公差是( )
,若在每相邻两项间各插入一个数,使之成等差数列,那么新的等差数列的公差是( )


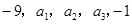 五个实数成等差数列,
五个实数成等差数列,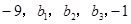 五个实数成等比数列,则
五个实数成等比数列,则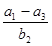 等于 ( )
等于 ( )




 的前
的前 项和为
项和为 ,若
,若 ,则
,则 = 。
= 。