题目内容
已知 为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( )
为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( )
 为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( )
为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( )| A.21 | B.20 | C.19 | D.18 |
B
试题分析:解:设{
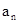 }的公差为d,由题意得
}的公差为d,由题意得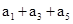 =
=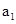 +
+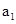 1+2d+
1+2d+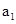 +4d=105,即
+4d=105,即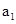 +2d=35,①
+2d=35,①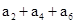 =
=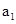 +d+
+d+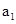 +3d+
+3d+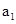 +5d=99,即
+5d=99,即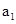 +3d=33,②
+3d=33,②由①②联立得
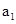 =39,d=-2,
=39,d=-2,∴
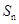 =39n+
=39n+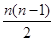 ×(-2)=-n2+40n=-(n-20)2+400,
×(-2)=-n2+40n=-(n-20)2+400,故当n=20时,
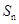 达到最大值400.
达到最大值400.故选B.
点评:求等差数列前n项和的最值问题可以转化为利用二次函数的性质求最值问题,但注意n取正整数这一条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
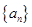 的前
的前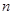 项和是
项和是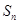 ,若
,若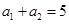 ,
,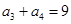 ,则
,则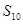 的值为( )
的值为( ) }满足
}满足 ,且
,且 ,则
,则 的值是( )
的值是( )

 的前
的前 项和记为
项和记为
 的各项为正,其前
的各项为正,其前 ,且
,且 ,又
,又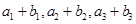 成等比数列,求
成等比数列,求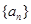 是等差数列,首项公差
是等差数列,首项公差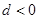 ,
,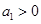 ,且
,且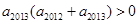 ,则使数列
,则使数列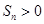 成立的最大自然数n是 ( )
成立的最大自然数n是 ( )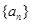 的前
的前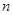 项和为
项和为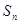 ,且
,且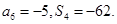
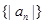 的前
的前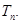
 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 成等比数列.
成等比数列. ,求数列
,求数列 的前
的前 项和
项和
 成等差数列,
成等差数列, 成等比数列 ,则
成等比数列 ,则 等于( )
等于( )