题目内容
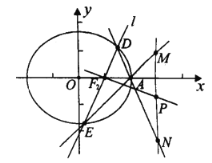
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上单调递减,求
上单调递减,求![]() 的取值范围;
的取值范围;
(2)若![]() 在
在![]() 处取得极值,判断当
处取得极值,判断当![]() 时,存在几条切线与直线
时,存在几条切线与直线![]() 平行,请说明理由;
平行,请说明理由;
(3)若![]() 有两个极值点
有两个极值点![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)答案见解析;(Ⅲ)证明见解析.
;(Ⅱ)答案见解析;(Ⅲ)证明见解析.
【解析】
(Ⅰ)由题意可得![]() 恒成立 ,构造函数,令
恒成立 ,构造函数,令![]() ,由导函数的解析式可知
,由导函数的解析式可知![]() 在
在![]() 递增,在
递增,在![]() 递减, 据此计算可得实数a的取值范围.
递减, 据此计算可得实数a的取值范围.
(Ⅱ) 由![]() 在
在![]() 处取得极值可得
处取得极值可得![]() .原问题等价于求解
.原问题等价于求解![]() 在区间
在区间![]() 内解的个数,结合导函数的解析式研究函数的单调性和函数在特殊点处的函数值即可确定切线的条数.而事实情况下检验
内解的个数,结合导函数的解析式研究函数的单调性和函数在特殊点处的函数值即可确定切线的条数.而事实情况下检验![]() 时函数
时函数![]() 不存在极值点,所以不存在满足题意的实数
不存在极值点,所以不存在满足题意的实数![]() ,也不存在满足题意的切线.
,也不存在满足题意的切线.
(Ⅲ)若函数有两个极值点![]() ,不妨设
,不妨设![]() ,易知
,易知![]() ,结合函数的解析式和零点的性质即可证得题中的不等式.
,结合函数的解析式和零点的性质即可证得题中的不等式.
(Ⅰ)由已知,![]() 恒成立
恒成立
令![]() ,
,
则![]() ,
,
![]() ,令
,令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,
,
故![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
![]() ,由
,由![]() 恒成立可得
恒成立可得![]() .
.
即当![]() 在
在![]() 上单调递减时,
上单调递减时,![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)![]() 在
在![]() 处取得极值,则
处取得极值,则![]() ,可得
,可得![]() .
.
令![]() ,即
,即 ![]() .
.
设![]() ,则
,则![]() .
.
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
注意到![]() ,
,![]() ,
,
则方程![]() 在
在![]() 内只有一个实数根,
内只有一个实数根,
即当![]() 时,只有一条斜率为
时,只有一条斜率为![]() 且与函数
且与函数![]() 图像相切的直线.
图像相切的直线.
但事实上,若![]() ,则
,则![]() ,
,
![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
且![]() ,故函数
,故函数![]() 在区间
在区间![]() 上恒成立,
上恒成立,
函数![]() 在区间
在区间![]() 上单调递减,即函数不存在极值点,
上单调递减,即函数不存在极值点,
即不存在满足题意的实数![]() ,也不存在满足题意的切线.
,也不存在满足题意的切线.
(Ⅲ)若函数有两个极值点![]() ,不妨设
,不妨设![]() ,
,
由(Ⅰ)可知![]() ,且:
,且:
![]() ①,
①,
![]() ②,
②,
由①-②得:![]() ,
,
即![]() ,
,
由①+②得:![]() ,
,
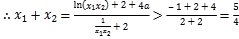 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某医院治疗白血病有甲、乙两套方案,现就70名患者治疗后复发的情况进行了统计,得到其等高条形图如图所示(其中采用甲、乙两种治疗方案的患者人数之比为![]() .
.
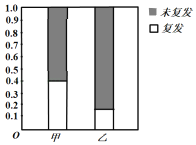
(1)补充完整![]() 列联表中的数据,并判断是否有
列联表中的数据,并判断是否有![]() 把握认为甲乙两套治疗方案对患者白血病复发有影响;
把握认为甲乙两套治疗方案对患者白血病复发有影响;
复发 | 未复发 | 总计 | |
甲方案 | |||
乙方案 | 2 | ||
总计 | 70 |
(2)为改进“甲方案”,按分层抽样组成了由5名患者构成的样本,求随机抽取2名患者恰好是复发患者和未复发患者各1名的概率.
附:
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 |
![]() ,
,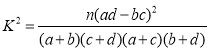 .
.