题目内容
【题目】在平面直角坐标系中,直线l:y![]() x﹣3经过椭圆
x﹣3经过椭圆![]() 1(a>b>0)的一个焦点,且点(0,b)到直线l的距离为2.
1(a>b>0)的一个焦点,且点(0,b)到直线l的距离为2.
(1)求椭圆E的方程;
(2)A、B、C是椭圆E上的三个动点,A与B关于原点对称,且|CA|=|CB|,求△ABC面积的最小值,并求此时点C的坐标.
【答案】(1)![]() (2)
(2)![]() ,
, ![]()
【解析】
(1)利用点到直线的距离公式可求出椭圆的方程;
(2)联立过![]() 直线与椭圆方程,利用弦长公式可求出
直线与椭圆方程,利用弦长公式可求出![]() ,由对称性可知,
,由对称性可知,![]() ,可得到
,可得到![]() 面积与直线
面积与直线![]() 斜率的关系,即可得出答案.
斜率的关系,即可得出答案.
(1)由题可知,![]() ,即
,即![]() ①
①
又![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
则有![]() ,
,
解得![]() ②
②
由①②得![]() ,
,
故椭圆![]() 的方程为:
的方程为:![]()
(2)由题可设过![]() ,
,![]() ,
,![]() ,
,![]() 两点的直线方程为:
两点的直线方程为:![]() ,
,
解方程组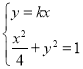 ,
,
可得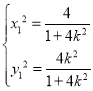
则有![]() ,
,
如图,
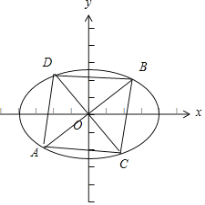
延长![]() 交椭圆于点
交椭圆于点![]() ,同理可得,
,同理可得,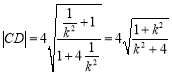 .
.
![]() ,
,
![]() .
.
由图形对称性可知,![]() .
.
令![]() .则有
.则有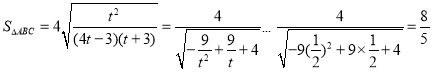 ,当且仅当
,当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
故![]() 面积的最小值为
面积的最小值为![]() ,此时,点
,此时,点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目