题目内容
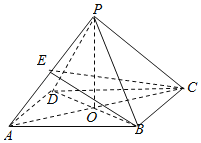
【题目】在四棱锥P﹣ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA![]() ,AC∩BD=O
,AC∩BD=O

(1)设平面ABP∩平面DCP=l,证明:l∥AB
(2)若E是PA的中点,求三棱锥P﹣BCE的体积VP﹣BCE.
【答案】(1)见解析(2)![]()
【解析】
(1)根据线面平行的判定定理、性质定理进行证明即可;
(2)根据菱形的性质、等腰三角形的性质,线面垂直的判定定理可以证明出BD⊥面PAC,因此可以得到BO是三棱锥B﹣PCE的高.再结合等边三角形的性质,结合勾股定理,三棱锥的体积公式进行求解即可.
证明:(1)因为AB∥DC,AB平面PDC,DC平面PDC,
所以AB∥平面PDC.
又平面ABP∩平面DCP=l,且AB面ABP,
所以l∥AB.
解:(2)因为底面是菱形,所以BD⊥AC.
因为PB=PD,且O是BD中点,所以BD⊥PO.
又PO∩AC=O,所以BD⊥面PAC.
所以BO是三棱锥B﹣PCE的高.
因为AO为边长为2的等边△ABD的中线,所以AO![]() .
.
因为PO为边长为2的等边△PBD的中线,所以PO![]() .
.
在△POA中,PA![]() ,AO
,AO![]() ,PO
,PO![]() ,
,
所以AO2+PO2=PA2,所以PO⊥AO.
所以![]() ,
,
因为E是线段PA的中点,所以![]() .
.
所以三棱锥P﹣BCE 的体积:
VP﹣BCE=VB﹣PCE![]() .
.

练习册系列答案
相关题目