题目内容
(本题满分15分) 如图,椭圆C: x2+3y2=3b2 (b>0).
(Ⅰ) 求椭圆C的离心率;
(Ⅱ) 若b=1,A,B是椭圆C上两点,且| AB | =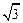 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
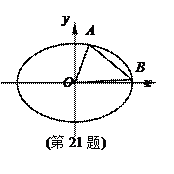
(Ⅰ) 求椭圆C的离心率;
(Ⅱ) 若b=1,A,B是椭圆C上两点,且| AB | =
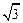 ,求△AOB面积的最大值.
,求△AOB面积的最大值.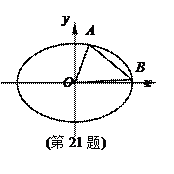
(Ⅰ)解:由x2+3y2=3b2 得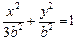 ,
,
所以e=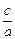 =
= =
=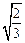 =
=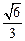 .
.
(Ⅱ)解:设A(x1,y1),B(x2,y2),△ABO的面积为S.
如果AB⊥x轴,由对称性不妨记A的坐标为(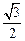 ,
,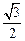 ),此时S=
),此时S= =
=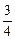 ;
;
如果AB不垂直于x轴,设直线AB的方程为y=kx+m,
由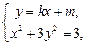 得x2+3(kx+m) 2=3,
得x2+3(kx+m) 2=3,
即 (1+3k2)x2+6kmx+3m2-3=0,又Δ=36k2m2-4(1+3k2) (3m2-3)>0,
所以 x1+x2=-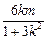 ,x1x2=
,x1x2=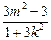 ,
,
(x1-x2)2=(x1+x2)2-4 x1x2=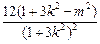 , ①
, ①
由 | AB |=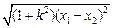 及 | AB |=
及 | AB |=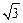 得
得
(x1-x2)2=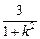 , ②
, ②
结合①,②得m2=(1+3k2)-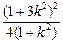 .又原点O到直线AB的距离为
.又原点O到直线AB的距离为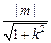 ,
,
所以S=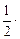
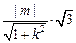 ,
,
因此S2=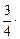
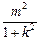 =
=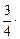 [
[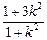 -
-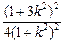 ]=
]=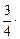 [-
[-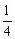 (
(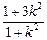 -2)2+1]
-2)2+1]
=-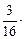 (
(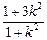 -2)2+
-2)2+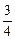 ≤
≤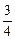 ,
,
故S≤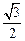 .当且仅当
.当且仅当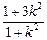 =2,即k=±1时上式取等号.又
=2,即k=±1时上式取等号.又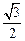 >
>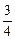 ,故S max=
,故S max=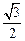 .
.
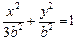 ,
,所以e=
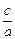 =
= =
=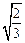 =
=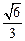 .
. (Ⅱ)解:设A(x1,y1),B(x2,y2),△ABO的面积为S.
如果AB⊥x轴,由对称性不妨记A的坐标为(
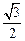 ,
,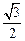 ),此时S=
),此时S= =
=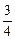 ;
;如果AB不垂直于x轴,设直线AB的方程为y=kx+m,
由
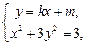 得x2+3(kx+m) 2=3,
得x2+3(kx+m) 2=3,即 (1+3k2)x2+6kmx+3m2-3=0,又Δ=36k2m2-4(1+3k2) (3m2-3)>0,
所以 x1+x2=-
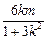 ,x1x2=
,x1x2=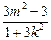 ,
,(x1-x2)2=(x1+x2)2-4 x1x2=
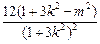 , ①
, ①由 | AB |=
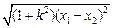 及 | AB |=
及 | AB |=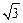 得
得(x1-x2)2=
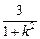 , ②
, ②结合①,②得m2=(1+3k2)-
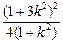 .又原点O到直线AB的距离为
.又原点O到直线AB的距离为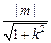 ,
,所以S=
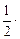
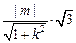 ,
,因此S2=
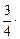
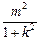 =
=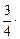 [
[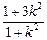 -
-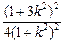 ]=
]=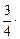 [-
[-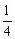 (
(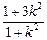 -2)2+1]
-2)2+1] =-
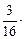 (
(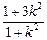 -2)2+
-2)2+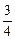 ≤
≤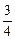 ,
,故S≤
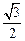 .当且仅当
.当且仅当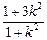 =2,即k=±1时上式取等号.又
=2,即k=±1时上式取等号.又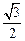 >
>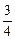 ,故S max=
,故S max=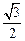 .
.略

练习册系列答案
相关题目
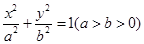 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 满足
满足 .
. ;
; 与椭圆相交于A,B两点.若直线
与椭圆相交于A,B两点.若直线 相交于M,N两点,且|MN|=
相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程.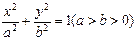 过点
过点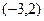 ,离心率为
,离心率为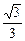 ,圆
,圆 的圆心为坐标原点,直径为椭圆的短轴,圆
的圆心为坐标原点,直径为椭圆的短轴,圆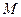 的方程为
的方程为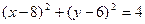 .过圆
.过圆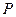 作圆
作圆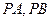 ,切点为
,切点为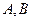 .
.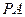 与圆
与圆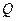 ,当弦
,当弦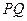 最大时,求直线
最大时,求直线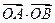 的最值.
的最值. 、
、 是椭圆
是椭圆 (
( )的两个焦点,
)的两个焦点,  是椭圆上任意一点,从任一焦点引
是椭圆上任意一点,从任一焦点引 的外角平分线的垂线,垂足为
的外角平分线的垂线,垂足为 , 则点
, 则点 . 圆
. 圆  . 椭圆
. 椭圆  . 双曲线
. 双曲线  . 抛物线
. 抛物线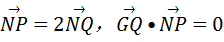 .
. 的离心率为( )
的离心率为( )
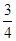


 及椭圆
及椭圆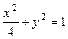 上任意一点
上任意一点 ,则
,则 最大值为 。
最大值为 。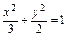 上一点P到左焦点的距离为
上一点P到左焦点的距离为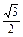 ,则P到左准线的距离为_________
,则P到左准线的距离为_________ 过椭圆
过椭圆 的右焦点,交椭圆于
的右焦点,交椭圆于 两点,求
两点,求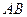 长
长