题目内容
已知圆M:(x+1)2+y2=8,定点N(1,0),点P为圆M上的动点,若Q在NP上,点G在MP上,且满足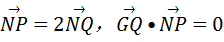 .
.
(I)求点G的轨迹C的方程;
(II)直线l过点P(0,2)且与曲线C相交于A、B两点,当△AOB面积取得最大值时,求直线l的方程.
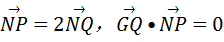 .
.(I)求点G的轨迹C的方程;
(II)直线l过点P(0,2)且与曲线C相交于A、B两点,当△AOB面积取得最大值时,求直线l的方程.
解:(I)∵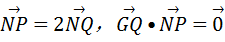
∴|GP|=|GN|
∴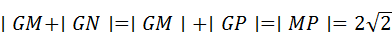
∵|MN|=2
∴G是以M,N为焦点的椭圆
设曲线C: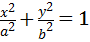 ,
,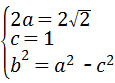 得a2=2,b2=1
得a2=2,b2=1
∴点G的轨迹C的方程为: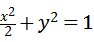 (6分)
(6分)
(II)由题意知直线l的斜率存在,
设直线l的方程为y=kx+2A(x1,y1)B(x2,y2)
由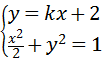 得:(1+2k2)x2+8kx+6=0
得:(1+2k2)x2+8kx+6=0
由直线l与椭圆相交于A、B两点,
∴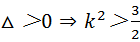
由根与系数关系得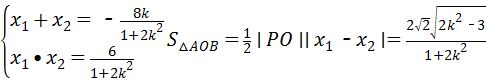
令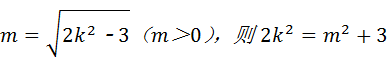
∴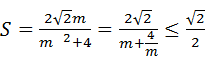
当且仅当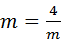 ,即m=2时,
,即m=2时,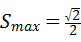 ,此时
,此时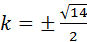
∴所求的直线方程为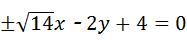 (13分)
(13分)
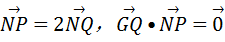
∴|GP|=|GN|
∴
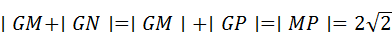
∵|MN|=2
∴G是以M,N为焦点的椭圆
设曲线C:
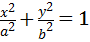 ,
,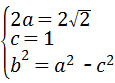 得a2=2,b2=1
得a2=2,b2=1∴点G的轨迹C的方程为:
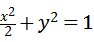 (6分)
(6分)(II)由题意知直线l的斜率存在,
设直线l的方程为y=kx+2A(x1,y1)B(x2,y2)
由
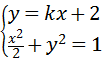 得:(1+2k2)x2+8kx+6=0
得:(1+2k2)x2+8kx+6=0由直线l与椭圆相交于A、B两点,
∴
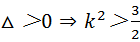
由根与系数关系得
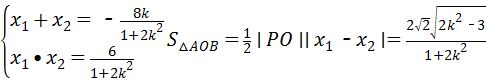
令
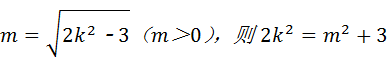
∴
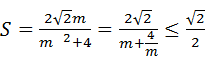
当且仅当
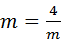 ,即m=2时,
,即m=2时,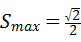 ,此时
,此时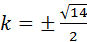
∴所求的直线方程为
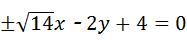 (13分)
(13分)略

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
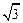 ,求△AOB面积的最大值.
,求△AOB面积的最大值.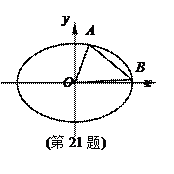
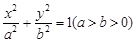 的左右焦点分别为
的左右焦点分别为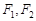 ,过焦点
,过焦点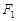 的倾斜角为
的倾斜角为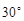 直线交椭圆于A,B两点,弦长
直线交椭圆于A,B两点,弦长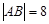 ,若三角形ABF2的内切圆的面积为
,若三角形ABF2的内切圆的面积为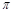 ,则椭圆的离心率为 ( )
,则椭圆的离心率为 ( )



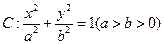 经过点M(-2,-1),离心率为
经过点M(-2,-1),离心率为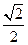 。过点M作倾斜角
。过点M作倾斜角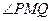 能否为直角?证明你的结论;
能否为直角?证明你的结论; 求这个定值。
求这个定值。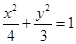 内有一点
内有一点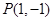 ,
,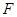 为椭圆的右焦点,在椭圆上有一点
为椭圆的右焦点,在椭圆上有一点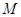 ,
,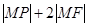 的值最小,则此最小值为 ( )
的值最小,则此最小值为 ( )



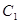 :
: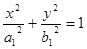 (
(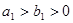 )和椭圆
)和椭圆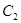 :
: 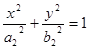
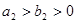 )的焦点相同且
)的焦点相同且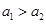 .给出如下四个结论:
.给出如下四个结论: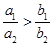 ;
;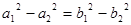 ; ④
; ④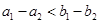 .
.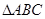 中,
中,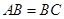 ,
,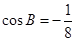 . 若以
. 若以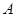 、
、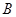 为焦点的双曲线经过点
为焦点的双曲线经过点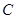 ,
,
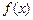 =
=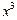 +
+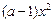 +3x+b的图象与x轴有三个不同交点,且交点的横坐标分别可作为抛物线、双曲线、椭圆的离心率,则实数a的取值范围是 .
+3x+b的图象与x轴有三个不同交点,且交点的横坐标分别可作为抛物线、双曲线、椭圆的离心率,则实数a的取值范围是 .