ЬтФПФкШн
ЁОЬтФПЁПФГЙЋдАгаИіГиЬСЃЌЦфаЮзДЮЊжБНЧЁїABCЃЌ![]() ЃЌABЕФГЄЮЊ2АйУзЃЌBCЕФГЄЮЊ1АйУз.
ЃЌABЕФГЄЮЊ2АйУзЃЌBCЕФГЄЮЊ1АйУз.
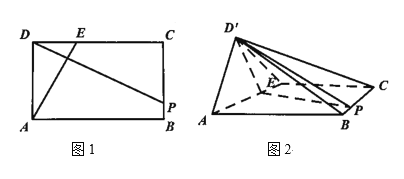
ЃЈ1ЃЉШєзМБИбјвЛХњЙЉгЮПЭЙлЩЭЕФгуЃЌЗжБ№дкABЁЂBCЁЂCAЩЯШЁЕуDЁЂEЁЂFЃЌШчЭМЃЈ1ЃЉЃЌЪЙЕУ![]() ЃЌ
ЃЌ![]() ЃЌдкЁїDEFФкЮЙЪГЃЌЧѓЕБЁїDEFЕФУцЛ§ШЁзюДѓжЕЪБEFЕФГЄЃЛ
ЃЌдкЁїDEFФкЮЙЪГЃЌЧѓЕБЁїDEFЕФУцЛ§ШЁзюДѓжЕЪБEFЕФГЄЃЛ
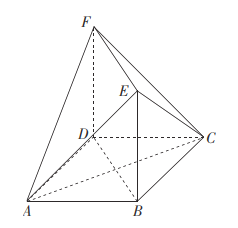
ЃЈ2ЃЉШєзМБИНЈдьвЛИіКЩЬСЃЌЗжБ№дкABЁЂBCЁЂCAЩЯШЁЕуDЁЂEЁЂFЃЌШчЭМЃЈ2ЃЉЃЌНЈдьЁїDEFСЌРШЃЈВЛПМТЧПэЖШЃЉЙЉгЮПЭанэЌЃЌЧвЪЙЁїDEFЮЊе§Ш§НЧаЮЃЌМЧ![]() ЃЌЧѓЁїDEFБпГЄЕФзюаЁжЕМАДЫЪБ
ЃЌЧѓЁїDEFБпГЄЕФзюаЁжЕМАДЫЪБ![]() ЕФжЕ.ЃЈОЋШЗЕН1УзКЭ0.1ЖШЃЉ
ЕФжЕ.ЃЈОЋШЗЕН1УзКЭ0.1ЖШЃЉ
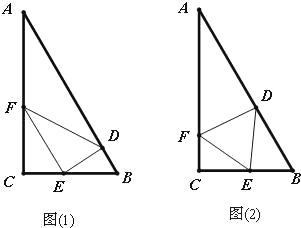
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉзюаЁжЕЪЧ65УзЃЌ
ЃЛЃЈ2ЃЉзюаЁжЕЪЧ65УзЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЩшEFЃНxЃЌдђПЩЧѓCEЃЌBEЃЌDEЃЌЧѓЕУSЁїDEF![]() xЃЈ1
xЃЈ1![]() ЃЉЃЌxЁЪЃЈ0ЃЌ2ЃЉЃЌгЩЛљБОВЛЕШЪНПЩЕУЃК
ЃЉЃЌxЁЪЃЈ0ЃЌ2ЃЉЃЌгЩЛљБОВЛЕШЪНПЩЕУЃК![]() ЃЈ1
ЃЈ1![]() ЃЉ
ЃЉ![]() ЃЈ
ЃЈ![]() ЃЉ2ЕБЧвНіЕБxЃН1ЪБЕШКХГЩСЂЃЌДгЖјПЩЧѓЕБЁїDEFЕФУцЛ§ШЁзюДѓжЕЪБEFЕФГЄЃЛ
ЃЉ2ЕБЧвНіЕБxЃН1ЪБЕШКХГЩСЂЃЌДгЖјПЩЧѓЕБЁїDEFЕФУцЛ§ШЁзюДѓжЕЪБEFЕФГЄЃЛ
ЃЈ2ЃЉЩшЕШБпШ§НЧаЮБпГЄЮЊEFЃНEDЃНDFЃНyЃЌдкЁїEBDжаЃЌгЩе§ЯвЖЈРэМАШ§НЧКЏЪ§ЕФаджЪПЩЕУy![]() 0.65ЃЌМДПЩЧѓЕУЁїDEFБпГЄЕФзюаЁжЕМАДЫЪБІСЕФжЕЃЎ
0.65ЃЌМДПЩЧѓЕУЁїDEFБпГЄЕФзюаЁжЕМАДЫЪБІСЕФжЕЃЎ
ЃЈ1ЃЉЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌЙЪ
ЃЌЙЪ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌSЁїDEF
ЃЌSЁїDEF![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
вђЮЊSЁїDEF![]() ЕБЧвНіЕБ
ЕБЧвНіЕБ![]() ЃЈМДEFГЄ100УзЃЉЪБЕШКХГЩСЂЃЌ
ЃЈМДEFГЄ100УзЃЉЪБЕШКХГЩСЂЃЌ
МДЃЈSЁїDEЃЉmax![]() .
.
ЃЈ2ЃЉЩшЕШБпШ§НЧаЮБпГЄЮЊ![]() ЃЌдкЁїEBDжаЃЌ
ЃЌдкЁїEBDжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гЩЬтвтПЩжЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
МД![]() ЃЌМДЁїDEFБпГЄЕФзюаЁжЕЪЧ65УзЃЌ
ЃЌМДЁїDEFБпГЄЕФзюаЁжЕЪЧ65УзЃЌ
ДЫЪБ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()

 аЁбЇЦкФЉГхДЬ100ЗжЯЕСаД№АИ
аЁбЇЦкФЉГхДЬ100ЗжЯЕСаД№АИ ЦкФЉИДЯАМьВтЯЕСаД№АИ
ЦкФЉИДЯАМьВтЯЕСаД№АИ ГЌФмбЇЕфЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
ГЌФмбЇЕфЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ ЛЦИд360ЖШЖЈжЦУмОэЯЕСаД№АИ
ЛЦИд360ЖШЖЈжЦУмОэЯЕСаД№АИ