题目内容
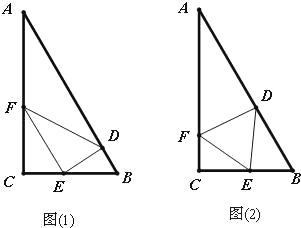
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,现将
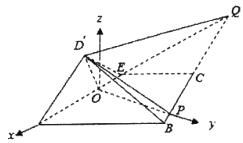
,现将![]() 沿
沿![]() 折到
折到![]() 的位置,连结
的位置,连结![]() ,
,![]() ,如图2
,如图2
(1)证明:![]() ;
;
(2)记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() .若二面角
.若二面角![]() 为
为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)建立坐标系证明![]() ,再由线面垂直的判定定理以及线面垂直的性质证明
,再由线面垂直的判定定理以及线面垂直的性质证明![]() ;
;
(2)根据公理![]() 得到平面
得到平面![]() 与平面
与平面![]() 的交线,再根据二面角定义得到二面角
的交线,再根据二面角定义得到二面角![]() 的平面角,建立空间直角坐标系,利用向量法求
的平面角,建立空间直角坐标系,利用向量法求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
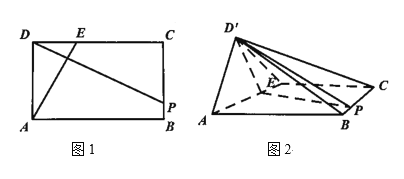
解:(1)证明:如图![]() ,线段
,线段![]() 交于点
交于点![]()
在![]() 中,由
中,由![]() ,
,![]() ,
,![]()
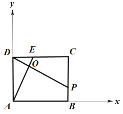
以点A为坐标原点,建立直角坐标系,则![]() ,
,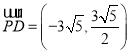
即![]()
![]() ,从而有
,从而有![]() ,
,![]() ,
,
即在图2中有![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面
平面![]() ,
,![]() ;
;
(2)延长![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]()
根据公理![]() 得到直线
得到直线![]() 即为
即为![]() ,再根据二面角定义得到
,再根据二面角定义得到![]() .
.
在平面![]() 内过点
内过点![]() 作底面垂线,
作底面垂线,![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 、及所作为
、及所作为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标
轴建立空间直角坐标
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由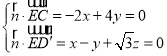 ,
,
取![]() ,得
,得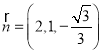 .
.
![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为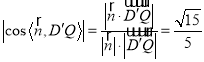 .
.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的![]() 城市和交通拥堵严重的
城市和交通拥堵严重的![]() 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:

(1)根据茎叶图,比较两城市满意度评分的平均值的大小(不要求计算具体值,给出结论即可);
(2)若得分不低于85分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此列联表,并据此样本分析是否有![]() 的把握认为城市拥堵与认可共享单车有关;
的把握认为城市拥堵与认可共享单车有关;
|
| 合计 | |
认可 | |||
不认可 | |||
合计 |
(3)若此样本中的![]() 城市和
城市和![]() 城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自
城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自![]() 城市的概率是多少?
城市的概率是多少?
(参考公式: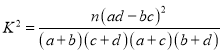 )
)
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |