题目内容
3.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的中心为O,它的一个顶点为(0,1),离心率为$\frac{{\sqrt{2}}}{2}$,过其右焦点的直线交该椭圆于A,B两点.(1)求这个椭圆的方程;
(2)若OA⊥OB,求△OAB的面积.
分析 (1)通过离心率,结合椭圆的几何量的关系,求解即可得到椭圆的方程.
(2)判断直线AB与x轴不垂直,设直线AB的斜率为k,写出直线AB的方程为y=k(x-1)与椭圆联立,设A(x1,y1),B(x2,y2),线段AB的中点为M(x0,y0),利用韦达定理结合OA⊥OB求出k的值,求出|AB|,求出直角△OAB斜边高为点O到直线AB的距离d,然后求解面积.
解答 解:(1)∵$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$∴${c^2}=\frac{1}{2}{a^2}$,…(1分)
依题意b=1,∴a2-c2=1,…(2分)
∴${a^2}-\frac{1}{2}{a^2}=1$∴a2=2,…(3分)
∴椭圆的方程为$\frac{x^2}{2}+\frac{y^2}{1}=1$;…(4分)
(2)椭圆的右焦点为(1,0),当直线AB与x轴垂直时,A,B的坐标为$(1,\frac{{\sqrt{2}}}{2}),(1,-\frac{{\sqrt{2}}}{2})$,
此时${k_{OA}}×{k_{OB}}=-\frac{1}{2}≠-1$∴直线AB与x轴不垂直,…(5分)
设直线AB的斜率为k,则直线AB的方程为y=k(x-1),
与$\frac{x^2}{2}+\frac{y^2}{1}=1$联立得(2k2+1)x2-4k2x+2k2-2=0,…(6分)
设A(x1,y1),B(x2,y2),线段AB的中点为M(x0,y0),
∴${x_1}+{x_2}=\frac{{4{k^2}}}{{2{k^2}+1}},\;{x_1}{x_2}=\frac{{2({k^2}-1)}}{{2{k^2}+1}}$,$M(\frac{{2{k^2}}}{{2{k^2}+1}},\frac{-k}{{2{k^2}+1}})$.…(7分)
∵OA⊥OB,∴kOA×kOB=0,∴x1x2+y1y2=0,
∴x1x2+k(x1-1)k(x2-1)=$({k^2}+1){x_1}{x_2}-{k^2}({x_1}+{x_2})+{k^2}=0$,
∴$\frac{{2({k^2}+1)({k^2}-1)}}{{2{k^2}+1}}-\frac{{4{k^4}}}{{2{k^2}+1}}+{k^2}=0$,∴k2=2∴$k=±\sqrt{2}$,…(9分)
∴|AB|2=4|OM|2=$4[{(\frac{{2{k^2}}}{{2{k^2}+1}})^2}+{(\frac{-k}{{2{k^2}+1}})^2}]=\frac{72}{25}$,∴$|AB|=\frac{{6\sqrt{2}}}{5}$.…(11分)
直角△OAB斜边高为点O到直线AB的距离d=$\frac{|k|}{{\sqrt{{k^2}+1}}}=\frac{{\sqrt{2}}}{{\sqrt{3}}}$,…(12分)
∴△OAB的面积为$\frac{1}{2}d|AB|=\frac{1}{2}×\frac{{\sqrt{2}}}{{\sqrt{3}}}×\frac{{6\sqrt{2}}}{5}=\frac{{2\sqrt{3}}}{5}$.…(13分)
点评 本题考查椭圆的标准方程的求法,直线与椭圆的综合应用,考查分析问题解决问题的能力以及计算能力.

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | a<c<b |
| A. | $-\frac{1}{2}+\frac{{\sqrt{3}}}{2}i$ | B. | $\frac{1}{2}+\frac{{\sqrt{3}}}{2}i$ | C. | $-\frac{1}{4}+\frac{{\sqrt{3}}}{4}i$ | D. | $\frac{1}{4}+\frac{{\sqrt{3}}}{4}i$ |
| A. | S15=150 | B. | a8=10 | C. | a16=20 | D. | a4+a12=20 |
| 类别 | A | B | C |
| 数量 | 4 | 3 | 2 |
(Ⅰ)从店中一次随机提取2辆车,求提取的两辆车为同一类型车的概率;
(Ⅱ)若一次性提取4辆车,其中A,B,C三种型号的车辆数分别记为a,b,c,记ξ为a,b,c的最大值,求ξ的分布列和数学期望.
| A. | 2015 | B. | -2015 | C. | 1 | D. | -1 |
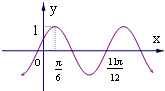 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象,如图所示,则将y=f(x)的图象向右平移$\frac{π}{3}$个单位后,得到的图象解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象,如图所示,则将y=f(x)的图象向右平移$\frac{π}{3}$个单位后,得到的图象解析式为( )| A. | y=sin(2x-$\frac{π}{6}$) | B. | y=cos2x | C. | y=sin(2x+$\frac{5π}{6}$) | D. | y=-cos2x |