题目内容
13．以坐标原点O为顶点，x轴的正半轴为始边，角α，β，θ的终边分别为OA，OB，OC，OC为∠AOB的角平分线，若$tanθ=\frac{1}{3}$，则tan（α+β）=（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
分析 由题意推出θ与α和β的关系，然后利用二倍角公式求解即可．
解答 解：以坐标原点O为顶点，x轴的正半轴为始边，角α，β，θ的终边分别为OA，OB，OC，OC为∠AOB的角平分线，
可得θ=$\frac{α+β}{2}$，
∵$tanθ=\frac{1}{3}$∴tan（α+β）=tan2θ=$\frac{2tanθ}{1-{tan}^{2}θ}$=$\frac{3}{4}$．
故选：D．
点评 本题考查二倍角公式的应用，三角函数的化简求值，考查计算能力．
练习册系列答案
相关题目
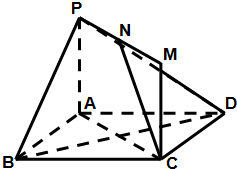如图，矩形ACMP和菱形ABCD所在的平面互相垂直，点N为PM的中点，