题目内容
(本小题满分14分)已知f(x)=ln(1+x)-x.
(Ⅰ)求f(x)的最大值;
(Ⅱ)数列{an}满足:an+1= 2f' (an) +2,且a1=2.5,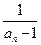 = bn,
= bn,
⑴数列{ bn+ }是等比数列 ⑵判断{an}是否为无穷数列。
}是等比数列 ⑵判断{an}是否为无穷数列。
(Ⅲ)对n∈N*,用⑴结论证明:ln(1+ +
+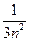 )<
)< ;
;
(Ⅰ)求f(x)的最大值;
(Ⅱ)数列{an}满足:an+1= 2f' (an) +2,且a1=2.5,
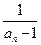 = bn,
= bn,⑴数列{ bn+
 }是等比数列 ⑵判断{an}是否为无穷数列。
}是等比数列 ⑵判断{an}是否为无穷数列。(Ⅲ)对n∈N*,用⑴结论证明:ln(1+
 +
+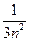 )<
)< ;
; (Ⅰ)极大值为f(0)=0,也是所求最大值;
(Ⅱ)(1)略
(2)数列{an}为无穷数列,证明略。
(Ⅲ)ln(1+ +
+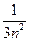 )<
)< ,证明略。
,证明略。
(Ⅱ)(1)略
(2)数列{an}为无穷数列,证明略。
(Ⅲ)ln(1+
 +
+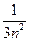 )<
)< ,证明略。
,证明略。⑴x>-1, f'(x)=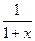 -1=
-1=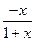 ,
,
∴极大值为f(0)=0,也是所求最大值;……………………4分
(Ⅱ)an+1= ,∴an+1-1=
,∴an+1-1=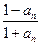 ,∴
,∴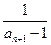 =-1-
=-1-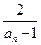 ,……………………5分
,……………………5分
则bn+1=-2 bn-1, ∴bn+1+ =-2(bn+
=-2(bn+ ), b1+
), b1+ ="1,"
="1,"
∴数列{ bn+ }是首项为1,公比为-2的等比数列,…………………7分
}是首项为1,公比为-2的等比数列,…………………7分
∴bn+ =(-2)n-1, ……………………8分
=(-2)n-1, ……………………8分
∴an=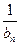 +1=
+1=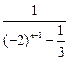 +1,……………………9分
+1,……………………9分
明显a1=2.5>-1,n≥2时(-2)n-1- <-2, ∴an>0>-1恒成立,
<-2, ∴an>0>-1恒成立,
∴数列{an}为无穷数列。……………………11分
(Ⅲ)由⑴ln(1+x) ≤x,∴ln(1+ +
+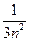 )< ln(1+
)< ln(1+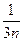 )3……………………12分
)3……………………12分
="3" ln(1+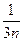 )≤3×
)≤3×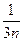 =
= 成立。 ………14分
成立。 ………14分
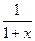 -1=
-1=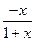 ,
,| x | (-1,0) | 0 | (0,+∞) |
| f'(x) | + | 0 | - |
| f(x) | ↗ | 极大值 | ↘ |
(Ⅱ)an+1=
 ,∴an+1-1=
,∴an+1-1=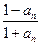 ,∴
,∴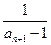 =-1-
=-1-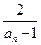 ,……………………5分
,……………………5分则bn+1=-2 bn-1, ∴bn+1+
 =-2(bn+
=-2(bn+ ), b1+
), b1+ ="1,"
="1," ∴数列{ bn+
 }是首项为1,公比为-2的等比数列,…………………7分
}是首项为1,公比为-2的等比数列,…………………7分∴bn+
 =(-2)n-1, ……………………8分
=(-2)n-1, ……………………8分∴an=
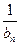 +1=
+1=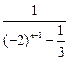 +1,……………………9分
+1,……………………9分明显a1=2.5>-1,n≥2时(-2)n-1-
 <-2, ∴an>0>-1恒成立,
<-2, ∴an>0>-1恒成立,∴数列{an}为无穷数列。……………………11分
(Ⅲ)由⑴ln(1+x) ≤x,∴ln(1+
 +
+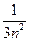 )< ln(1+
)< ln(1+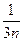 )3……………………12分
)3……………………12分="3" ln(1+
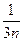 )≤3×
)≤3×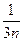 =
= 成立。 ………14分
成立。 ………14分
练习册系列答案
相关题目
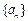 中,若
中,若 ,
,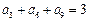 ,则
,则 = 。
= 。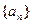 满足
满足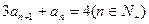 ,且
,且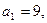 前n项和为
前n项和为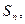 则满足不等式
则满足不等式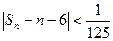 的最小整数n是( )
的最小整数n是( )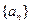 中,
中,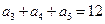 ,则
,则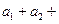 。。。
。。。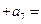 ( )
( )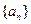 中,
中,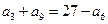 ,
, 表示数列
表示数列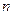 项和,则
项和,则 ( )
( )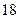


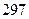
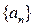 中,
中,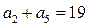 ,
, ,则
,则 ________
________  和等比数列
和等比数列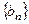 中,已知
中,已知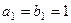 ,
, ,
, ;
; 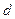 和
和 ;
;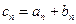 ,求数列
,求数列 的通项公式
的通项公式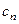 及前
及前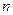 项和
项和 .
.