题目内容
直线l：y=x+b与抛物线C：x2=4y相切于点A．
（Ⅰ）求实数b的值，及点A的坐标；
（Ⅱ）求过点B（0，-1）的抛物线C的切线方程．
（Ⅰ）求实数b的值，及点A的坐标；
（Ⅱ）求过点B（0，-1）的抛物线C的切线方程．
（Ⅰ）直线l：y=x+b与抛物线C：x2=4y联立，消去y，可得x2-4x-4b=0．（*）
因为直线l与抛物线C相切，所以△=（-4）2-4×（-4b）=0，解得b=-1；
代入方程（*）即为x2-4x+4=0，解得x=2，y=1，故点A（2，1）．
（Ⅱ）设过点B（0，-1）的抛物线C的切线方程为y=kx-1．
与抛物线C：x2=4y联立，消去y，可得x2-4kx+4=0，
因为直线l与抛物线C相切，所以△=（-4k）2-4×4=0，解得k=±1，
所以过点B（0，-1）的抛物线C的切线方程为y=±x-1．
因为直线l与抛物线C相切，所以△=（-4）2-4×（-4b）=0，解得b=-1；
代入方程（*）即为x2-4x+4=0，解得x=2，y=1，故点A（2，1）．
（Ⅱ）设过点B（0，-1）的抛物线C的切线方程为y=kx-1．
与抛物线C：x2=4y联立，消去y，可得x2-4kx+4=0，
因为直线l与抛物线C相切，所以△=（-4k）2-4×4=0，解得k=±1，
所以过点B（0，-1）的抛物线C的切线方程为y=±x-1．
练习册系列答案
活力课时同步练习册系列答案
相关题目
中，已知抛物线
：
，在此抛物线上一点
到焦点的距离是3.
轴交于
的直线
与抛物线
、
两点．是否存在这样的
满足
，若存在，求
（
）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形.
上任意一点，过F作TF的垂线交椭圆C于点P，Q.
最小时，求点T的坐标.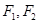
为椭圆C：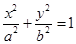
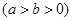的左、右焦点，D，E是椭圆的两个顶点，椭圆的离心率
，
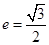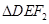的面积为
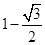.若点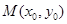
在椭圆C上，则点
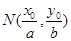称为点M的一个“椭圆”，直线
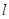与椭圆交于A，B两点，A，B两点的“椭圆”分别为P，Q.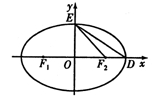
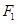的直线