题目内容
如图,己知矩形ABCD的两个顶点A、D位于x轴上,另两个顶点B、C位于抛物线y=4-x2在x轴上方的曲线上,求这个矩形ABCD面积的最大值.


设点B(x,4-x2)(O<x≤2)…(1分)
则S=2x(4-x2)=2x3+8x…(3分)
∴S′=-6x2+8,∴S′=-6x2+8=0即x=
所以x=
时,S=2x3+8x取得最大值为
即矩形ABCD面积的最大值是…(14分)
则S=2x(4-x2)=2x3+8x…(3分)
∴S′=-6x2+8,∴S′=-6x2+8=0即x=
| 2 |
| 3 |
| 3 |
所以x=
| 2 |
| 3 |
| 3 |
| 32 |
| 9 |
| 3 |
即矩形ABCD面积的最大值是…(14分)

练习册系列答案
相关题目
 a2.
a2.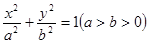 的右焦点为
的右焦点为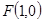 ,离心率
,离心率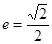 ,
,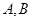 是椭圆上的动点.
是椭圆上的动点.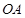 与
与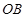 的斜率乘积
的斜率乘积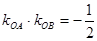 ,动点
,动点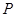 满足
满足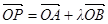 ,(其中实数
,(其中实数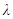 为常数).问是否存在两个定点
为常数).问是否存在两个定点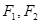 ,使得
,使得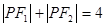 ?若存在,求
?若存在,求