题目内容
如图,设点A(x0,y0)为抛物线y2=
上位于第一象限内的一动点,点B(0,y1)在y轴正半轴上,且|OA|=|OB|,直线AB交x轴于点P(x2,0).
(Ⅰ)试用x0表示y1;
(Ⅱ)试用x0表示x2;
(Ⅲ)当点A沿抛物线无限趋近于原点O时,求点P的极限坐标.

| x |
| 2 |
(Ⅰ)试用x0表示y1;
(Ⅱ)试用x0表示x2;
(Ⅲ)当点A沿抛物线无限趋近于原点O时,求点P的极限坐标.

(Ⅰ)|OA|=
=
=
,
∴y1=|OB|=
.
(Ⅱ)kAB=
,
=
,
=
,
直线AB的方程为
y=
x+
,
令y=0,得
x2=
.
(Ⅲ)
x2=
=1,
故当点A沿抛物线无限趋近于原点O时,求点P的极限坐标是(1,0).
|
|
| 1 |
| 2 |
4
|
∴y1=|OB|=
| 1 |
| 2 |
4
|
(Ⅱ)kAB=
| y1-y0 |
| -x0 |
=
| ||||||||||
| -x0 |
=
| ||||
| 2x0 |
直线AB的方程为
y=
| ||||
| 2x0 |
| 1 |
| 2 |
| 4x02+2x0 |
令y=0,得
x2=
2x0+1+
| ||
| 2 |
(Ⅲ)
| lim |
| x→0+ |
| lim |
| x→0+ |
2x0+1+
| ||
| 2 |
故当点A沿抛物线无限趋近于原点O时,求点P的极限坐标是(1,0).

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 a2.
a2. 的三个顶点在抛物线
的三个顶点在抛物线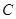 :
: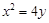 上,
上, 为抛物线
为抛物线 为
为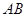 的中点,
的中点,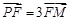 ;
;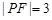 ,求点
,求点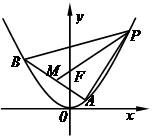
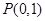 与抛物线
与抛物线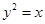 有且只有一个交点的直线有( )
有且只有一个交点的直线有( )