题目内容
12.设a为大于1的常数,函数f(x)=$\left\{\begin{array}{l}{log_a}x,x>0\\{a^x},x≤0\end{array}$,若关于x的方程f2(x)-bf(x)=0恰有三个不同的实数解,则实数b的取值范围是( )| A. | 0<b≤1 | B. | 0<b<1 | C. | 0≤b≤1 | D. | b>1 |
分析 由题意可得f(x)=0或f(x)=b,从而可得f(x)=b在(-∞,0]上必须有且只有一个解,从而解得.
解答 解:f2(x)-bf(x)=f(x)(f(x)-b)=0,
∴f(x)=0或f(x)=b,
由f(x)=0解得,x=1;
若x>0,则由f(x)=b解得,
x=ab,
又∵关于x的方程f2(x)-bf(x)=0恰有三个不同的实数解,
∴f(x)=b在(-∞,0]上必须有且只有一个解,
又∵x∈(-∞,0]时,ax∈(0,1];
故0<b≤1;
故选A.
点评 本题考查了函数的零点与方程的根的关系应用及分段函数的应用,属于中档题.

练习册系列答案
相关题目
7.变量x,y 满足$\left\{\begin{array}{l}y≥-1\\ x-y≥2\\ 3x+y≤14\end{array}\right.$,若使z=ax+y取得最大值的最优解有无穷多个,实数a的集合是( )
| A. | {-3,0 } | B. | { 3,-1} | C. | { 0,1 } | D. | {-3,0,1 } |
2.教室里有6盏灯,由3个开关控制,每个开关控制2盏灯,则不同的照明方法有( )
| A. | 63种 | B. | 31种 | C. | 8种 | D. | 7种 |
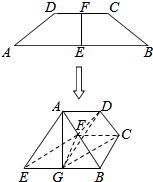 在等腰梯形ABCD中,E,F分别是AB,CD的中点,AB=4,CD=2,AD=BC=$\sqrt{2}$,现将梯形AEFD沿EF折起,并记平面AEFD与平面BEFC所成二面角的平面角为θ,BE中点为G.
在等腰梯形ABCD中,E,F分别是AB,CD的中点,AB=4,CD=2,AD=BC=$\sqrt{2}$,现将梯形AEFD沿EF折起,并记平面AEFD与平面BEFC所成二面角的平面角为θ,BE中点为G.