题目内容
17.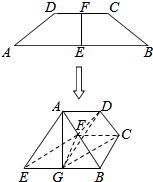 在等腰梯形ABCD中,E,F分别是AB,CD的中点,AB=4,CD=2,AD=BC=$\sqrt{2}$,现将梯形AEFD沿EF折起,并记平面AEFD与平面BEFC所成二面角的平面角为θ,BE中点为G.
在等腰梯形ABCD中,E,F分别是AB,CD的中点,AB=4,CD=2,AD=BC=$\sqrt{2}$,现将梯形AEFD沿EF折起,并记平面AEFD与平面BEFC所成二面角的平面角为θ,BE中点为G.(1)当θ=60°时,求证:AG⊥平面AEFC;
(2)当三棱锥D-CFG的体积取得最大值时,求DG与平面AEFD所成角的正切值.
分析 (1)由已知AF=BF,∠AFB=60°,G为FB的中点,可得AG⊥FB①再由E、F分别是CD、AB的中点,可得EF⊥AB,于是EF⊥AF,EF⊥BF,则EF⊥平面ABF,进而可得AG⊥EF②,结合①②根据直线与平面垂直的判定定理可证AG⊥平面BCEF.
(2)根据三棱锥D-CFG的底面是个常数,则只需要高最大即可,得到DF⊥平面BCFE,从而得到直线和平面所成的平面角,结合三角形的边角关系进行求解即可.
解答 解:(Ⅰ)∵AE⊥EF,BE⊥EF,
∴∠AEB是二面角AEFD与平面BEFC的平面角,即∠AEB=θ,
∵AF=BF,∠AFB=60°,△AFB为等边三角形.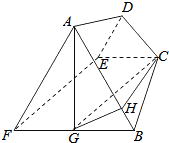
又G为FB的中点,所以AG⊥FB.
在等腰梯形ABCD中,
∵E、F分别是CD、AB的中点,
∴EF⊥AB.于是EF⊥AF,EF⊥BF,则EF⊥平面ABF,
∴AG⊥EF.
又EF与FB交于一点F,
∴AG⊥平面BCEF.
(2)∵△CFG的面积是个常数,
∴要使三棱锥D-CFG的体积取得最大,
则只需D到平面EFG的距离最大,即DF⊥平面BCFE即可,
此时平面AEFD⊥平面BCFE,
∵EG⊥平面AEDF,
∴∠GDE就是DG与平面AEFD所成的角,
则tan∠GDE=$\frac{EG}{DE}$,
∵EG=$\frac{1}{2}BE=\frac{1}{2}×2=1$,DF=$\frac{1}{2}DC=\frac{1}{2}×2=1$,AD=BC=$\sqrt{2}$,
∴EF=1,
则DF=$\sqrt{2}$,
即tan∠GDE=$\frac{EG}{DE}$=$\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
点评 本题主要考查空间线面关系中的垂直关系:线面垂直的判定的运用、线面角的度求解,要求考生具备一定的空间想象能力、推理论证能力和运算求解能力.

 名校课堂系列答案
名校课堂系列答案| A. | 0<b≤1 | B. | 0<b<1 | C. | 0≤b≤1 | D. | b>1 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
| A. | y=2sinx | B. | y=cos2x | C. | y=sin$\frac{1}{2}$x | D. | y=2cos(x+$\frac{π}{2}$) |