题目内容
20.设sin2α=-sinα,$α∈(\frac{π}{2},π)$,则tan2α的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
分析 由条件利用二倍角的正弦公式,求得cosα的值,可得α的值,再利用诱导公式求得诱导公式tan2α的值.
解答 解:∵sin2α=2sinαcosα=-sinα,$α∈(\frac{π}{2},π)$,∴cosα=-$\frac{1}{2}$,∴α=$\frac{2π}{3}$,
则tan2α=tan$\frac{4π}{3}$=tan$\frac{π}{3}$=$\sqrt{3}$,
故选:D.
点评 本题主要考查二倍角的正弦公式,根据三角函数的值求角,以及诱导公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若集合M={1,2,3},N={x|0<x≤3,x∈R},则下列论断正确的是( )
| A. | x∈M是x∈N的充分不必要条件 | B. | x∈M是x∈N的必要不充分条件 | ||
| C. | x∈M是x∈N 的充分必要条件 | D. | x∈M是x∈N的既不充分也不必要条件 |
8.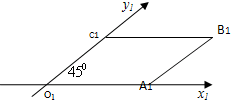 如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )
如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )
 如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )
如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )| A. | 1 | B. | 4 | C. | 1或4 | D. | 不能确定 |
5.若函数f(x)唯一的一个零点同时在区间(0,8)、(0,6)、(0,4)、(0,2)内,那么下列命题中正确的是( )
| A. | 函数f(x)在区间(0,1)内有零点 | B. | 函数f(x)在区间(0,1)或(1,2)内有零点 | ||
| C. | 函数f(x)在区间[2,8)内无零点 | D. | 函数f(x)在区间(1,8)内无零点 |
12. 在电脑游戏中,“主角”的生命机会往往被预先设定.如某枪战游戏,“主角”被设置生命6次,每次生命承受射击8次(即被击中8次就失去一次生命机会),假设射击为单发射击,如图是为“主角”耗用生命机会的过程设计的一个程序框图,请问判断框内应该填( )
在电脑游戏中,“主角”的生命机会往往被预先设定.如某枪战游戏,“主角”被设置生命6次,每次生命承受射击8次(即被击中8次就失去一次生命机会),假设射击为单发射击,如图是为“主角”耗用生命机会的过程设计的一个程序框图,请问判断框内应该填( )
 在电脑游戏中,“主角”的生命机会往往被预先设定.如某枪战游戏,“主角”被设置生命6次,每次生命承受射击8次(即被击中8次就失去一次生命机会),假设射击为单发射击,如图是为“主角”耗用生命机会的过程设计的一个程序框图,请问判断框内应该填( )
在电脑游戏中,“主角”的生命机会往往被预先设定.如某枪战游戏,“主角”被设置生命6次,每次生命承受射击8次(即被击中8次就失去一次生命机会),假设射击为单发射击,如图是为“主角”耗用生命机会的过程设计的一个程序框图,请问判断框内应该填( )| A. | i<6 | B. | i<8 | C. | i>48 | D. | i<48 |
10.在△ABC中,设A(5,3),B(4,5),C(1,1),则△ABC的面积等于( )
| A. | 15 | B. | 10 | C. | 7.5 | D. | 5 |
 把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图的三角形数表:
把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图的三角形数表: