题目内容
10．在△ABC中，设A（5，3），B（4，5），C（1，1），则△ABC的面积等于（ ）| A． | 15 | B． | 10 | C． | 7.5 | D． | 5 |
分析 利用两点间的距离公式求出三角形的边长，判断三角形是直角三角形，即可得到结论．
解答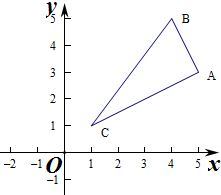 
解：∵A（5，3），B（4，5），C（1，1），
∴|AB|=$\sqrt{（5-4）^{2}+（3-5）^{2}}$=$\sqrt{1+4}$=$\sqrt{5}$，
|BC|=$\sqrt{（4-1）^{2}+（5-1）^{2}}$=$\sqrt{9+16}=\sqrt{25}$=5，
|AC|=$\sqrt{（5-1）^{2}+（3-1）^{2}}$=$\sqrt{16+4}=\sqrt{20}$=2$\sqrt{5}$，
∵|AB|2+|AC|2=|BC|2，
∴△ABC是以∠A为直角的直角三角形，
则△ABC的面积S=$\frac{1}{2}$|AC||AB|=$\frac{1}{2}×2\sqrt{5}×\sqrt{5}$=5，
故选：D
点评 本题主要考查三角形面积的计算，利用两点间的距离公式求出三角形的边长，判断三角形是直角三角形是解决本题的关键．
练习册系列答案
相关题目
20．设sin2α=-sinα，$α∈（\frac{π}{2}，π）$，则tan2α的值是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | 1 | D． | $\sqrt{3}$ |
2．已知正四棱柱ABCD-A1B1C1D1中，AB=2，CC1=2$\sqrt{2}$，E为CC1的中点，则点C到平面BED的距离为（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |