题目内容
4.已知函数f(x)满足f(x+4)=f(x),且当-1<x≤3时,f(x)=$\left\{\begin{array}{l}{m\sqrt{1-{x}^{2}},x∈(-1,1]}\\{1-|x-2|,x∈(1,3]}\end{array}\right.$.其中m>0,若方程3f(x)-x=0恰好有5个根,则实数m的取值范围是( )| A. | ($\frac{\sqrt{15}}{3}$,$\sqrt{7}$) | B. | ($\frac{\sqrt{15}}{3}$,$\frac{8}{3}$) | C. | ($\frac{4}{3}$,$\sqrt{7}$) | D. | ( $\frac{4}{3}$,$\frac{8}{3}$) |
分析 根据条件求出函数是周期为4的函数,作出两个函数的图象,利用数形结合结合直线和曲线的相切问题,即可得到结论.
解答 解:由f(x+4)=f(x),得函数f(x)是周期为4的函数,
若方程3f(x)-x=0恰好有5个根,
即方程f(x)-$\frac{x}{3}$=0恰好有5个根,
即f(x)=$\frac{x}{3}$恰好有5个根,
即函数f(x)与g(x)=$\frac{x}{3}$恰好有5个交点,
作出函数f(x)与g(x)的图象,
当0<x<3时,两个函数有3个交点
当x>0时,设y=g(x)=log4|x|=log4x,
则g(3)=log43<1,f(3)=f(1)=1,
g(5)=log45>1,故当x>0,两个函数有3个交点,
则要使函数f(x)与g(x)=$\frac{x}{3}$恰好有5个交点,
则只需要保证在3<x<4时,有两个交点,同时在7<x<8时,没有交点即可,
∵f(x+4)=f(x),∴f(x)=f(x-4),
∴当3<x<4时,-1<x-4<0,此时f(x)=f(x-4)=m$\sqrt{1-(x-4)^{2}}$,
当直线y=$\frac{x}{3}$与y=m$\sqrt{1-(x-4)^{2}}$相切时,
满足$\frac{x}{3}$=m$\sqrt{1-(x-4)^{2}}$,
平方得(1+9m2)x2-72m2x+135m2=0,
则判别式△=(-72m2)2-4(1+9m2)×135m2=0,
整理得m2=$\frac{15}{9}$,解得m=$\frac{\sqrt{15}}{3}$,此时两个函数有4个交点,
当7<x<8时,3<x-4<4,此时f(x)=f(x-4)=m$\sqrt{1-(x-4-4)^{2}}$=m$\sqrt{1-(x-8)^{2}}$,
当直线y=$\frac{x}{3}$与y=m$\sqrt{1-(x-8)^{2}}$相切时,
满足$\frac{x}{3}$=m$\sqrt{1-(x-8)^{2}}$,
平方得(1+9m2)x2-16×9m2x+63×9m2=0,
则判别式△=(-16×9m2)2-4(1+9m2)×63×9m2=0,
整理得m2=7,解得m=$\sqrt{7}$,此时两个函数有6个交点,
故若函数f(x)与g(x)=$\frac{x}{3}$恰好有5个交点,
则实数m的取值范围$\frac{\sqrt{15}}{3}$<m<$\sqrt{7}$,即($\frac{\sqrt{15}}{3}$,$\sqrt{7}$),
故选:A
点评 本题主要考查函数交点个数的判断,利用条件判断函数的周期性,利用数形结合是解决本题的关键.运算量大,综合性较强难度较大.

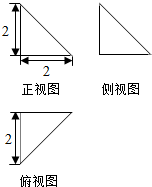
| A. | 4$\sqrt{3}$π | B. | $\frac{4\sqrt{3}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{4\sqrt{2}π}{3}$ |
| A. | (-3,-3,0) | B. | (0,0,3) | C. | (0,-3,-3) | D. | (0,0,-3) |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分条件 | D. | 既不充分也不必要条件 |