题目内容
18.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{b}$=(1,$\sqrt{3}$),$\overrightarrow{b}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=-3,则向量$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为$\frac{7}{2}$.分析 由$\overrightarrow{b}$=(1,$\sqrt{3}$)求得$|\overrightarrow{b}|$,展开$\overrightarrow{b}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=-3,求出$\overrightarrow{a}•\overrightarrow{b}$,则向量$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影可求.
解答 解:∵$\overrightarrow{b}$=(1,$\sqrt{3}$),∴$|\overrightarrow{b}|=\sqrt{{1}^{2}+(\sqrt{3})^{2}}=2$,
再由$\overrightarrow{b}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=-3,得$|\overrightarrow{b}{|}^{2}-\overrightarrow{a}•\overrightarrow{b}=-3$,即4-$\overrightarrow{a}•\overrightarrow{b}=-3$,
∴$\overrightarrow{a}•\overrightarrow{b}=7$,
∴向量$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为$|\overrightarrow{a}|cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{7}{2}$.
故答案为:$\frac{7}{2}$.
点评 本题考查了平面向量的数量积运算,考查了数量积的几何意义,是中档题.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
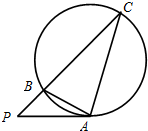 如图,过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,PB=3,AB=4,则AC=8.
如图,过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,PB=3,AB=4,则AC=8.