题目内容
19.已知$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$是同一平面内的三个向量,其中$\overrightarrow{a}$=(2,1).(1)若|$\overrightarrow{c}$|=3$\sqrt{5}$,且$\overrightarrow{c}$∥$\overrightarrow{a}$,求$\overrightarrow{c}$的坐标;
(2)若|$\overrightarrow{b}$|=$\frac{\sqrt{5}}{2}$,且$\overrightarrow{a}$+2$\overrightarrow{b}$与2$\overrightarrow{a}$-$\overrightarrow{b}$垂直,求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ.
分析 (1)因为$\overrightarrow{c}$∥$\overrightarrow{a}$,所以设$\overrightarrow{c}$=$λ\overrightarrow{a}$=(2λ,λ),再由|$\overrightarrow{c}$|=3$\sqrt{5}$,得到λ.
(2)$\overrightarrow{a}$+2$\overrightarrow{b}$与2$\overrightarrow{a}$-$\overrightarrow{b}$垂直得到数量积为0,求出$\overrightarrow{a}•\overrightarrow{b}$,再由数量积公式求出向量的夹角θ.
解答 解:(1)因为|$\overrightarrow{c}$|=3$\sqrt{5}$,且$\overrightarrow{c}$∥$\overrightarrow{a}$,设$\overrightarrow{c}$=$λ\overrightarrow{a}$=(2λ,λ),则$|\overrightarrow{c}|$=$\sqrt{5{λ}^{2}}$=3$\sqrt{5}$,解得λ=±3,
所以$\overrightarrow{c}$=(6,3)或(-6,-3);
(2)因为|$\overrightarrow{b}$|=$\frac{\sqrt{5}}{2}$,且$\overrightarrow{a}$+2$\overrightarrow{b}$与2$\overrightarrow{a}$-$\overrightarrow{b}$垂直,所以
($\overrightarrow{a}$+2$\overrightarrow{b}$)•(2$\overrightarrow{a}$-$\overrightarrow{b}$)=0 即2${\overrightarrow{a}}^{2}-2{\overrightarrow{b}}^{2}+3\overrightarrow{a}•\overrightarrow{b}$=0,∴2×5-2×$\frac{5}{4}$-3$\overrightarrow{a}•\overrightarrow{b}$=0,
解得$\overrightarrow{a}•\overrightarrow{b}$=$-\frac{5}{2}$…(10分)
所以cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=-1,又θ∈[0,π],所以θ=π,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为π.
点评 本题考查平面向量的坐标运算和数量积判断两个平面垂直的条件的灵活运用,是基础题.解题时要认真审题,仔细解答

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | {x∈R|x2-1=0} | B. | {x|x>6或x<1} | C. | {(x,y)|x2+y2=0} | D. | {x|x>6且x<1} |
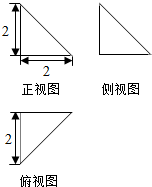
| A. | 4$\sqrt{3}$π | B. | $\frac{4\sqrt{3}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{4\sqrt{2}π}{3}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |