题目内容
20．函数$y={（\frac{1}{3}）^x}$与函数$f（x）={log_{\frac{1}{2}}}$x的图象的交点的个数为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 分别画出函数$y={（\frac{1}{3}）^x}$（红色曲线）与函数$f（x）={log_{\frac{1}{2}}}$x（蓝色曲线）的图象，如图所示，由图象可知答案．
解答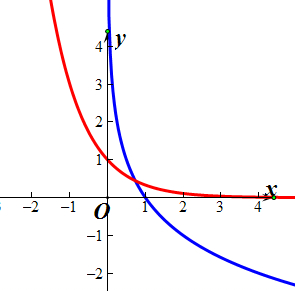 
解：分别画出函数$y={（\frac{1}{3}）^x}$（红色曲线）与函数$f（x）={log_{\frac{1}{2}}}$x（蓝色曲线）的图象，如图所示
由图象可知，函数$y={（\frac{1}{3}）^x}$与函数$f（x）={log_{\frac{1}{2}}}$x的图象的交点的个数有1个，
故选：B
点评 本题考查了指数函数和对数函数的图象，属于基础题．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
10．下列集合中，结果是空集的是（ ）
| A． | {x∈R|x2-1=0} | B． | {x|x＞6或x＜1} | C． | {（x，y）|x2+y2=0} | D． | {x|x＞6且x＜1} |
15．设点P是Z轴上一点，且点P到M（1，0，2）与点N（1，-3，1）的距离相等，则点P的坐标是（ ）
| A． | （-3，-3，0） | B． | （0，0，3） | C． | （0，-3，-3） | D． | （0，0，-3） |
5．某超市从2014年甲、乙两种酸奶的日销售量（单位：箱）的数据中分別随机抽取100个．整理得到数据分组及频率分布表和频率分布直方图：
（Ⅰ）写出频率分布直方图1中的a的值；并作出甲种酸奶日销售量的频率分布直方图；
（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为s${\;}_{1}^{2}$，s${\;}_{2}^{2}$，试比较s${\;}_{1}^{2}$与s${\;}_{2}^{2}$的大小；（只需写出结论）
（Ⅲ）假设同一组中的每个数据可用该该组区间的中点值代替，试估计乙种酸奶在未来一个月（按30天计箅）的销售量总量．
| 分组（日销售量） | 频率（甲种酸奶） |
| [0，10] | 0.10 |
| （10，20] | 0.20 |
| （20，30] | 0.30 |
| （30，40] | 0.25 |
| （40，50] | 0.15 |
（Ⅰ）写出频率分布直方图1中的a的值；并作出甲种酸奶日销售量的频率分布直方图；
（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为s${\;}_{1}^{2}$，s${\;}_{2}^{2}$，试比较s${\;}_{1}^{2}$与s${\;}_{2}^{2}$的大小；（只需写出结论）
（Ⅲ）假设同一组中的每个数据可用该该组区间的中点值代替，试估计乙种酸奶在未来一个月（按30天计箅）的销售量总量．