题目内容
设直线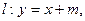 双曲线
双曲线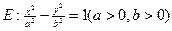 ,双曲线的离心率为
,双曲线的离心率为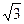 ,
, 与
与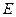 交于
交于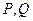 两点,直线
两点,直线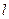 与
与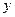 轴交于点
轴交于点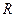 ,且
,且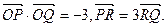
(1)证明: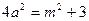 ;(2)求双曲线
;(2)求双曲线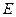 的方程;(3)若点
的方程;(3)若点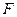 是双曲线
是双曲线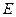 的右焦点,
的右焦点,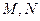 是双曲线上两点,且
是双曲线上两点,且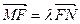 ,求实数
,求实数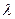 的取值范围.
的取值范围.
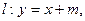 双曲线
双曲线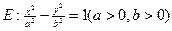 ,双曲线的离心率为
,双曲线的离心率为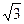 ,
,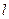 与
与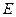 交于
交于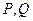 两点,直线
两点,直线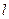 与
与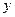 轴交于点
轴交于点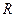 ,且
,且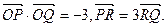
(1)证明:
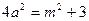 ;(2)求双曲线
;(2)求双曲线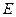 的方程;(3)若点
的方程;(3)若点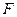 是双曲线
是双曲线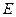 的右焦点,
的右焦点,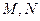 是双曲线上两点,且
是双曲线上两点,且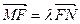 ,求实数
,求实数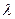 的取值范围.
的取值范围.(Ⅰ) 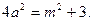 (Ⅱ)
(Ⅱ) 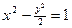 (Ⅲ)
(Ⅲ)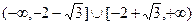
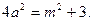 (Ⅱ)
(Ⅱ) 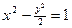 (Ⅲ)
(Ⅲ)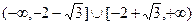
(1) 双曲线的离心率为
双曲线的离心率为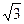 ,
,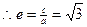 ,从而
,从而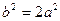 .双曲线的方程可化为
.双曲线的方程可化为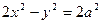 . 设
. 设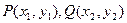
由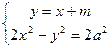 得:
得: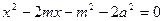
则有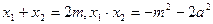 从而
从而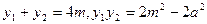
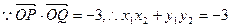
则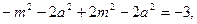 即
即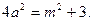
(2)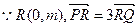 ,
, 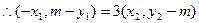
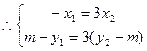 ,由
,由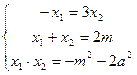 得
得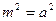
由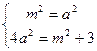 得
得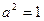 则
则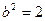
故双曲线的方程为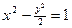
(3)易知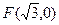 ,设
,设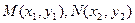 .由
.由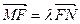 得:
得: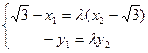
设直线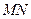 的方程为
的方程为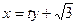 .由
.由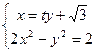 得:
得: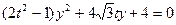
则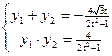 ,消去
,消去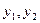 得:
得: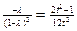
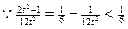 ,
, 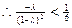 , 解得
, 解得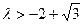 或
或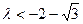
当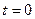 时,可求出
时,可求出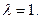
当直线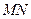 与
与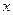 轴重合时,可求出
轴重合时,可求出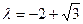 或
或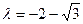
故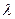 的取值范围是
的取值范围是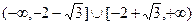 .
.
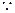 双曲线的离心率为
双曲线的离心率为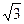 ,
,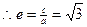 ,从而
,从而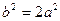 .双曲线的方程可化为
.双曲线的方程可化为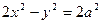 . 设
. 设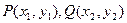
由
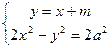 得:
得: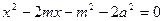
则有
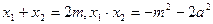 从而
从而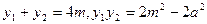
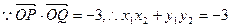
则
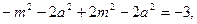 即
即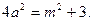
(2)
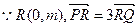 ,
, 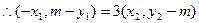
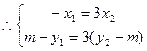 ,由
,由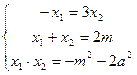 得
得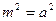
由
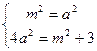 得
得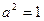 则
则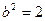
故双曲线的方程为
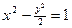
(3)易知
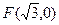 ,设
,设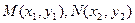 .由
.由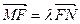 得:
得: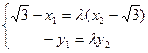
设直线
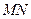 的方程为
的方程为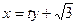 .由
.由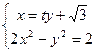 得:
得: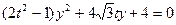
则
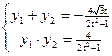 ,消去
,消去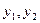 得:
得: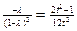
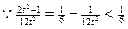 ,
, 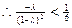 , 解得
, 解得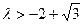 或
或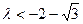
当
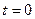 时,可求出
时,可求出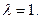
当直线
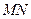 与
与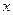 轴重合时,可求出
轴重合时,可求出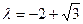 或
或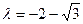
故
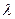 的取值范围是
的取值范围是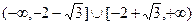 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,相交于M、N两点.
,相交于M、N两点. 的取值范围;
的取值范围;  ;
; .
.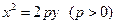 上的一点(m,1)到焦点的距离为
上的一点(m,1)到焦点的距离为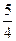 .点
.点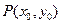 是抛物线上任意一点(除去顶点),过点
是抛物线上任意一点(除去顶点),过点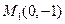 与
与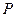 的直线和抛物线交于点
的直线和抛物线交于点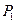 ,过点
,过点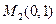 与的
与的 .分别以点
.分别以点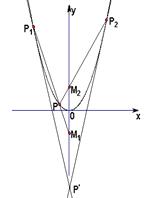
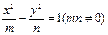 的离心率为2,有一个焦点与椭圆
的离心率为2,有一个焦点与椭圆 的焦点重合,则m的值为( )
的焦点重合,则m的值为( )



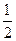 |AA1|.椭圆的一条弦AC交双曲线于E,设
|AA1|.椭圆的一条弦AC交双曲线于E,设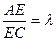 ,当
,当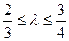 时,求双曲线的离心率e的取值范围.
时,求双曲线的离心率e的取值范围.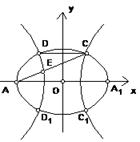
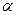 的始边为x轴的非负半轴,终边为射线l:y=
的始边为x轴的非负半轴,终边为射线l:y=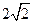 x (x≥0).
x (x≥0).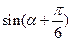 的值;
的值;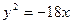 上,圆A与y轴相切,又与另一圆
上,圆A与y轴相切,又与另一圆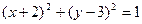 相外切,求圆A的方程.
相外切,求圆A的方程.
 (
(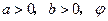 为参数)上的点
为参数)上的点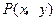 ,求
,求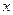 ,
,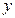 的取值范围; ⑵
的取值范围; ⑵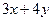 的取值范围.
的取值范围.