题目内容
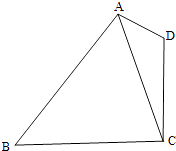
【题目】如图，在平面四边形ABCD中，AD=1，CD=2，AC= 
． 
（1）求cos∠CAD的值；
（2）若cos∠BAD=﹣ 
，sin∠CBA= 
，求BC的长．
【答案】
（1）解： cos∠CAD= 
= 
= 
．
（2）解：∵cos∠BAD=﹣ 
，
∴sin∠BAD= 
= 
，
∵cos∠CAD= ，
∴sin∠CAD= 
= 
∴sin∠BAC=sin（∠BAD﹣∠CAD）=sin∠BADcos∠CAD﹣cos∠BADsin∠CAD= × + × = 
，
∴由正弦定理知 
= 
，
∴BC= sin∠BAC= 
× =3
【解析】（1）利用余弦定理，利用已知条件求得cos∠CAD的值．（2）根据cos∠CAD，cos∠BAD的值分别，求得sin∠BAD和sin∠CAD，进而利用两角和公式求得sin∠BAC的值，最后利用正弦定理求得BC．
练习册系列答案
相关题目
【题目】连锁经营公司所属5个零售店某月的销售额利润资料如表：
商品名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
（参考公式： 
= 
= 
， 
= 
﹣ x）
（1）画出销售额和利润额的散点图
（2）若销售额和利润额具有相关关系，试计算利润额y对销售额x的回归直线方程．
（3）估计要达到1000万元的利润额，销售额约为多少万元．
