题目内容
【题目】已知函数f(x)=(x﹣1)|x﹣a|﹣x﹣2a(x∈R).
(1)若a=﹣1,求方程f(x)=1的解集;
(2)若 ![]() ,试判断函数y=f(x)在R上的零点个数,并求此时y=f(x)所有零点之和的取值范围.
,试判断函数y=f(x)在R上的零点个数,并求此时y=f(x)所有零点之和的取值范围.
【答案】
(1)解:方法一:
当a=﹣1时, 
由f(x)=1得 ![]() 或
或 ![]()
解得 x=0,1,﹣2,即解集为{0,1,﹣2}.
方法二:当a=﹣1时,由f(x)=1得:(x﹣1)|x+1|﹣(x﹣1)=0(x﹣1)(|x+1|﹣1)=0
∴得x=1或|x+1|=1∴x=1或x=0或x=﹣2
即解集为{0,1,﹣2}.
(2)解: 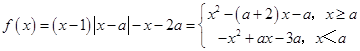
当x≥a时,令x2﹣(a+2)x﹣a=0,∵ ![]() ,
,
∴△=a2+8a+4=(a+4)2﹣12>0
得 ![]() ,
, ![]()
且 ![]()
先判断2﹣a,与 ![]() 大小:
大小:
∵ ![]() ,即a<x1<x2,故当x≥a时,f(x)存在两个零点.
,即a<x1<x2,故当x≥a时,f(x)存在两个零点.
当x<a时,令﹣x2+ax﹣3a=0,即x2﹣ax+3a=0得∵ ![]() ,
,
∴△=a2﹣12a=(a﹣6)2﹣36>0
得 ![]() ,
, ![]()
同上可判断x3<a<x4,故x<a时,f(x)存在一个零点.
综上可知当 ![]() 时,f(x)存在三个不同零点.
时,f(x)存在三个不同零点.
且 
设 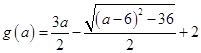 ,易知g(a)在
,易知g(a)在 ![]() 上单调递增,
上单调递增,
故g(a)∈(0,2)∴x1+x2+x3∈(0,2)
【解析】(1)方法一:化简分段函数,分段求解方程的根即可,方法二:当a=﹣1时,利用f(x)=1化简求解即可.(2)化简分段函数,通过当x≥a时,当x<a时,求出函数的零点,推出 ![]() ,构造函数,利用函数的单调性,求解即可.
,构造函数,利用函数的单调性,求解即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目