Question

【题目】椭圆 =1（a＞b＞0）的离心率为 ，右焦点到直线x+y+ =0的距离为2 ． （Ⅰ） 求椭圆的方程；
（Ⅱ） 过点M（0，﹣1）作直线l交椭圆于A，B两点，交x轴于N点，满足 =﹣ ，求直线l的方程．

Answer 1

【答案】解：（Ⅰ）∵椭圆的离心率为 ，右焦点到直线x+y+ =0的距离为2 ， ∴
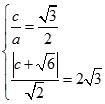
∴c= ，a=2 ，
∴b= ，
∴椭圆的方程为 ；
（Ⅱ）设A （x1 ， y1），B（x2 ， y2），N（x0 ， 0）
∵ =﹣ ，
∴（x1﹣x0 ， y1）=﹣ （x2﹣x0 ， y2）
∴y1=﹣ y2①
易知直线斜率不存在时或斜率为0时①不成立
于是设直线l的方程为y=kx﹣1（k≠0）．
与椭圆方程联立，消去x可得（4k2+1）y2+2y+1﹣8k2=0②
∴y1+y2=﹣ ③y1y2= ④
由①③可得y2= ，y1=﹣ 代入④整理可得：8k4+k2﹣9=0
∴k2=1
此时②为5y2+2y﹣7=0，判别式大于0
∴直线l的方程为y=±x﹣1
【解析】（Ⅰ）根据圆的离心率为 ，右焦点到直线x+y+ =0的距离为2 ，建立方程组，可求椭圆的方程；（Ⅱ）设A （x1 ， y1），B（x2 ， y2），N（x0 ， 0），利用 =﹣ ，可得（x1﹣x0 ， y1）=﹣ （x2﹣x0 ， y2），设直线l的方程为y=kx﹣1（k≠0），与椭圆方程联立，消去x可得（4k2+1）y2+2y+1﹣8k2=0，由此即可求得直线l的方程．