题目内容
对于各项均为整数的数列 ,如果
,如果 为完全平方数,则称数列
为完全平方数,则称数列 具有“P性质”,如果数列
具有“P性质”,如果数列 不具有“P性质”,只要存在与
不具有“P性质”,只要存在与 不是同一数列的
不是同一数列的 ,且
,且 同时满足下面两个条件:①
同时满足下面两个条件:① 是
是 的一个排列;②数列
的一个排列;②数列 具有“P性质”,则称数列
具有“P性质”,则称数列 具有“变换P性质”,下面三个数列:
具有“变换P性质”,下面三个数列:
①数列1,2,3,4,5; ②数列1,2,3, ,11,12; ③数列 的前n项和为
的前n项和为 .
.
其中具有“P性质”或“变换P性质”的有( )
 ,如果
,如果 为完全平方数,则称数列
为完全平方数,则称数列 具有“P性质”,如果数列
具有“P性质”,如果数列 不具有“P性质”,只要存在与
不具有“P性质”,只要存在与 不是同一数列的
不是同一数列的 ,且
,且 同时满足下面两个条件:①
同时满足下面两个条件:① 是
是 的一个排列;②数列
的一个排列;②数列 具有“P性质”,则称数列
具有“P性质”,则称数列 具有“变换P性质”,下面三个数列:
具有“变换P性质”,下面三个数列:①数列1,2,3,4,5; ②数列1,2,3, ,11,12; ③数列
 的前n项和为
的前n项和为 .
.其中具有“P性质”或“变换P性质”的有( )
| A.③ | B.①③ | C.①② | D.①②③ |
D
试题分析:解:①因为
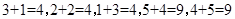 ,所以数列1,2,3,4,5具有“变换P性质”;
,所以数列1,2,3,4,5具有“变换P性质”;②类似地,由于数列
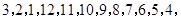 具有“P性质”,所以数列具有“变换P性质”;
具有“P性质”,所以数列具有“变换P性质”;③当
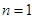 时,
时,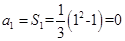
当
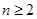 时,
时,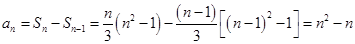
上式对
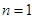 也成立,所以对任意
也成立,所以对任意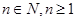 ,都有
,都有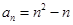
所以有
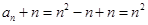
所以数列
 具有“P性质”
具有“P性质”综上,具有“P性质”或“变换P性质”的有①②③
故选D.
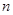 项和公式求数列的通项公式.
项和公式求数列的通项公式.
练习册系列答案
相关题目
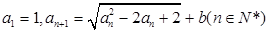
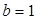 ,求
,求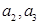 及数列
及数列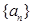 的通项公式;
的通项公式;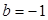 ,问:是否存在实数
,问:是否存在实数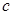 使得
使得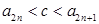 对所有
对所有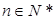 成立?证明你的结论.
成立?证明你的结论.
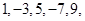 ……的一个通项公式为( ).
……的一个通项公式为( ).
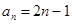
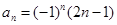

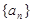 中,
中,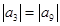 公差
公差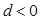 ,那么使
,那么使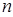 项和
项和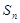 最大的
最大的


 满足
满足
 ,
, ,则
,则 的最小值为
的最小值为



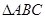 是边长为1的正三角形,曲线
是边长为1的正三角形,曲线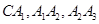 是分别以
是分别以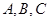 为圆心,
为圆心,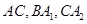 为半径画的弧,曲线
为半径画的弧,曲线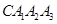 记为螺旋线旋第一圈.然后又以
记为螺旋线旋第一圈.然后又以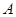 为圆心
为圆心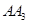 为半径画弧,
为半径画弧,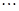
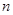 圈,则所得螺旋线的长度
圈,则所得螺旋线的长度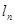 为( )
为( )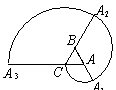

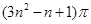


 中,
中, ,则
,则 .
.