题目内容
【题目】已知圆![]() 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足![]() .
.
(I)求点G的轨迹C的方程
(II)过点(2,0)作直线![]() ,与曲线C交于A、B两点,O是坐标原点,设
,与曲线C交于A、B两点,O是坐标原点,设![]() 是否存在这样的直线
是否存在这样的直线![]() ,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线
,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线![]() 的方程若不存在,试说明理由.
的方程若不存在,试说明理由.
【答案】(1) ![]() ;(2)存在直线
;(2)存在直线![]() 使得四边形OASB的对角线相等.
使得四边形OASB的对角线相等.
【解析】本试题主要是考查了圆锥曲线的轨迹方程的求解,借助于向量的工具,来表示,同时能运用联立方程组的思想表示出直线与圆锥曲线的交点问题的关系式,结合向量得到直线方程。
(1)根据局题中的向量的关系式,运用坐标法表示得到轨迹方程
(2)设直线方程与椭圆的方程联立,然后结合题中的图形的特点和向量的关系式,得到直线关系式,确定直线的存在与否。
解:(1)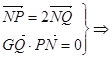 Q为PN的中点且GQ⊥PN
Q为PN的中点且GQ⊥PN
![]() GQ为PN的中垂线
GQ为PN的中垂线![]() |PG|=|GN|---------------------------------(3分)
|PG|=|GN|---------------------------------(3分)
∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长![]() ,半焦距
,半焦距![]() ,∴短半轴长b=2,∴点G的轨迹方程是
,∴短半轴长b=2,∴点G的轨迹方程是![]() ---------(6分)
---------(6分)
(2)因为![]() ,所以四边形OASB为平行四边形,若存在l使得|
,所以四边形OASB为平行四边形,若存在l使得|![]() |=|
|=|![]() |,则四边形OASB为矩形
|,则四边形OASB为矩形![]() ……………(7分)
……………(7分)
若l的斜率不存在,直线l的方程为x=2,由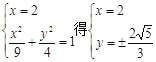
![]() 矛盾,……………(8分)
矛盾,……………(8分)
故l的斜率存在,设l的方程为![]()
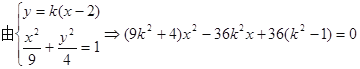 ……………………(10分)
……………………(10分)
![]() ①………………………(11分)
①………………………(11分)
![]()
![]() ② ………… ……………(12分)
② ………… ……………(12分)
把①、②代入![]() ∴存在直线
∴存在直线![]() 使得四边形OASB的对角线相等. ……… …………………… ……………(14分)
使得四边形OASB的对角线相等. ……… …………………… ……………(14分)

【题目】为及时了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位30岁到40岁的公务员,得到情况如表:
(1)完成表格,并判断是否有99%以上的把握认为“生二胎意愿与性别有关”,并说明理由;
(2)现把以上频率当作概率,若从社会上随机独立抽取三位30岁到40岁的男公务员访问,求这三人中至少有一人有意愿生二胎的概率.
(3)已知15位有意愿生二胎的女性公务员中有两位来自省妇联,该部门打算从这15位有意愿生二胎的女性公务员中随机邀请两位来参加座谈,设邀请的2人中来自省女联的人数为X,求X的公布列及数学期望E(X).
男性公务员 | 女性公务员 | 总计 | |
有意愿生二胎 | 30 | 15 | |
无意愿生二胎 | 20 | 25 | |
总计 |
附: ![]()
P(k2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |

