题目内容
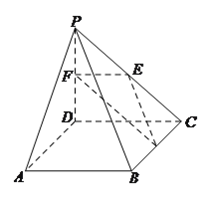
【题目】如图,长方体![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.

(1)求证:直线![]() ∥平面
∥平面![]() ;
;
(2)求证:平面![]()
![]() 平面
平面![]() ;
;
(3)求证:直线![]()
![]() 平面
平面![]() .
.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)利用三角形中位线的性质证明PO//![]() ,进而得到线
,进而得到线![]() ∥平面
∥平面![]() ;
;
(2)由底面ABCD是正方形,则AC![]() BD,再由
BD,再由![]() ,得到AC
,得到AC![]() 面
面![]() ,这样在平面PAC内找到了两条相交直线和平面垂直,问题得到解决;
,这样在平面PAC内找到了两条相交直线和平面垂直,问题得到解决;
(3)△PB1C中,先求出三边的长度,利用勾股定理可得![]()
![]() PC,同理
PC,同理![]()
![]() PA,之后根据线面垂直的判定定理证得结果.
PA,之后根据线面垂直的判定定理证得结果.
(1)设AC和BD交于点O,连PO,由P,O分别是![]() ,
,
BD的中点,故PO//![]() ,所以直线
,所以直线![]() ∥平面
∥平面![]()
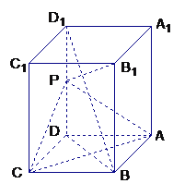
(2)长方体![]() 中,
中,![]() ,底面ABCD是正方形,则AC
,底面ABCD是正方形,则AC![]() BD
BD
又![]()
![]() 面ABCD,则
面ABCD,则![]()
![]() AC, BD∩
AC, BD∩![]() =D
=D
所以AC![]() 面
面![]() ,AC
,AC![]() 面
面![]() ,则平面
,则平面![]()
![]() 平面
平面![]()
(3)PC2=2,PB12=3,B1C2=5,所以△PB1C是直角三角形。![]()
![]() PC,
PC,
同理![]()
![]() PA,PC∩PA=P 所以直线
PA,PC∩PA=P 所以直线![]()
![]() 平面
平面![]() 。
。

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目