题目内容
在数列{an}中,a1=2,a4=8,且满足an+2=2an+1-an(n∈N*)
(1)求数列{an}的通项公式
(2)设bn=2n-1·an,求数列{bn}的前n项和sn
(1)求数列{an}的通项公式
(2)设bn=2n-1·an,求数列{bn}的前n项和sn
(1)an=2+2(n—1)=2n
(2)bn=2n-1·2n=n·2n
sn=(n-1)2n+1+2
(2)bn=2n-1·2n=n·2n
sn=(n-1)2n+1+2
解:(1)∵an+2=2an+1-an(n∈N*)
∴an+an+2=2an+1
∴{an}为等差数列
设公差为d,由题意得8=2+3d,∴d="2 " ∴an=2+2(n—1)=2n
(2)∵bn=2n-1·2n=n·2n
∴sn=b1+b2+b3+…+bn=1·21+2·22+3·23+…+n·2n ①
∴2sn=1·22+2·23+…(n—1)·2n+n·2n+1 ②
①—②得-sn=21+22+23+…+2n—n·2n+1=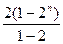 -n·2n+1=2n+1-2- n·2n+1=(1-n)2n+1-2
-n·2n+1=2n+1-2- n·2n+1=(1-n)2n+1-2
∴sn=(n-1)2n+1+2
∴an+an+2=2an+1
∴{an}为等差数列
设公差为d,由题意得8=2+3d,∴d="2 " ∴an=2+2(n—1)=2n
(2)∵bn=2n-1·2n=n·2n
∴sn=b1+b2+b3+…+bn=1·21+2·22+3·23+…+n·2n ①
∴2sn=1·22+2·23+…(n—1)·2n+n·2n+1 ②
①—②得-sn=21+22+23+…+2n—n·2n+1=
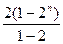 -n·2n+1=2n+1-2- n·2n+1=(1-n)2n+1-2
-n·2n+1=2n+1-2- n·2n+1=(1-n)2n+1-2∴sn=(n-1)2n+1+2

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 满足
满足 且
且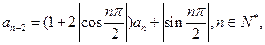
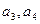 ;
;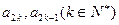 ;
;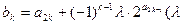 为非零整数),试确定
为非零整数),试确定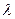 的值,使得对任意
的值,使得对任意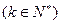 都有
都有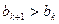 成立。
成立。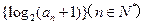 为等差数列,且
为等差数列,且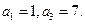 求
求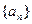 的通项公式;
的通项公式;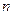 项和.
项和.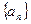 中,前三项分别为
中,前三项分别为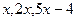 ,前
,前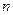 项和为
项和为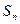 , (1)、求
, (1)、求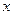 和
和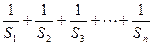 ,证明T<1
,证明T<1 ,
, ,
, ,
,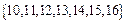 ,……,
,……,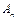 ;由自然数的立方构成下列数组:
;由自然数的立方构成下列数组: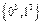 ,
,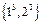 ,
,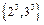 ,
,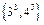 ,……,
,……,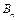 ,则
,则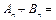 .
. 对任意的p、q
对任意的p、q 有ap+aq=ap+q,若a1=
有ap+aq=ap+q,若a1=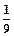 ,则a36="__________."
,则a36="__________." 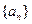 为等差数列,其前n项和为
为等差数列,其前n项和为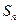 ,已知
,已知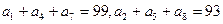 ,若对任意
,若对任意 都有
都有 成立,则k的值为( )
成立,则k的值为( )