题目内容
已知函数f(x)=lnx-ax(a∈R).
(1)求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在[1,2]上的最小值.
(1)求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在[1,2]上的最小值.
(1)单调增区间是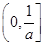 ,单调减区间是
,单调减区间是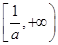 (2)当0<a<ln2时,最小值是-a;当a≥ln2时,最小值是ln2-2a.
(2)当0<a<ln2时,最小值是-a;当a≥ln2时,最小值是ln2-2a.
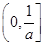 ,单调减区间是
,单调减区间是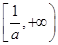 (2)当0<a<ln2时,最小值是-a;当a≥ln2时,最小值是ln2-2a.
(2)当0<a<ln2时,最小值是-a;当a≥ln2时,最小值是ln2-2a.①知函数解析式求单调区间,实质是求f′(x)>0,f′(x)<0的解区间,并注意定义域;
②先研究f(x)在[1,2]上的单调性,再确定最值是端点值还是极值;
③由于解析式中含有参数a,要对参数a进行分类讨论.
规范解答:解:(1)f′(x)=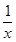 -a(x>0).(1分)
-a(x>0).(1分)
①当a≤0时,f′(x)=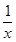 -a≥0,即函数f(x)的单调增区间是(0,+∞).(3分)
-a≥0,即函数f(x)的单调增区间是(0,+∞).(3分)
②当a>0时,令f′(x)=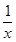 -a=0,得x=
-a=0,得x=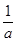 ,当0<x<
,当0<x< 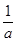 时,f′(x)=
时,f′(x)=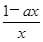 >0,当x>
>0,当x> 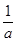 时,f′(x)=
时,f′(x)=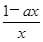 <0,所以函数f(x)的单调增区间是
<0,所以函数f(x)的单调增区间是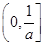 ,单调减区间是
,单调减区间是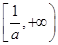 .(6分)
.(6分)
(2)①当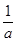 ≤1,即a≥1时,函数f(x)在区间[1,2]上是减函数,
≤1,即a≥1时,函数f(x)在区间[1,2]上是减函数,
所以f(x)的最小值是f(2)=ln2-2a.(8分)
②当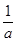 ≥2,即0<a≤
≥2,即0<a≤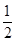 时,函数f(x)在区间[1,2]上是增函数,
时,函数f(x)在区间[1,2]上是增函数,
所以f(x)的最小值是f(1)=-a.(10分)
③当1<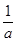 <2,即
<2,即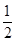 <a<1时,函数f(x)在区间
<a<1时,函数f(x)在区间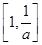 上是增函数,在区间
上是增函数,在区间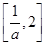 上是减函数,
上是减函数,
又f(2)-f(1)=ln2-a,
所以当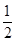 <a<ln2时,最小值是f(1)=-a;
<a<ln2时,最小值是f(1)=-a;
当ln2≤a<1时,最小值是f(2)=ln2-2a.(12分)
综上可知,当0<a<ln2时,最小值是-a;
当a≥ln2时,最小值是ln2-2a.(14分)
②先研究f(x)在[1,2]上的单调性,再确定最值是端点值还是极值;
③由于解析式中含有参数a,要对参数a进行分类讨论.
规范解答:解:(1)f′(x)=
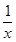 -a(x>0).(1分)
-a(x>0).(1分)①当a≤0时,f′(x)=
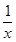 -a≥0,即函数f(x)的单调增区间是(0,+∞).(3分)
-a≥0,即函数f(x)的单调增区间是(0,+∞).(3分)②当a>0时,令f′(x)=
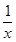 -a=0,得x=
-a=0,得x=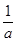 ,当0<x<
,当0<x< 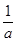 时,f′(x)=
时,f′(x)=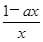 >0,当x>
>0,当x> 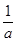 时,f′(x)=
时,f′(x)=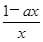 <0,所以函数f(x)的单调增区间是
<0,所以函数f(x)的单调增区间是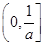 ,单调减区间是
,单调减区间是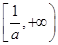 .(6分)
.(6分)(2)①当
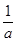 ≤1,即a≥1时,函数f(x)在区间[1,2]上是减函数,
≤1,即a≥1时,函数f(x)在区间[1,2]上是减函数,所以f(x)的最小值是f(2)=ln2-2a.(8分)
②当
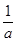 ≥2,即0<a≤
≥2,即0<a≤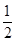 时,函数f(x)在区间[1,2]上是增函数,
时,函数f(x)在区间[1,2]上是增函数,所以f(x)的最小值是f(1)=-a.(10分)
③当1<
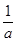 <2,即
<2,即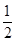 <a<1时,函数f(x)在区间
<a<1时,函数f(x)在区间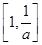 上是增函数,在区间
上是增函数,在区间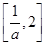 上是减函数,
上是减函数,又f(2)-f(1)=ln2-a,
所以当
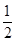 <a<ln2时,最小值是f(1)=-a;
<a<ln2时,最小值是f(1)=-a;当ln2≤a<1时,最小值是f(2)=ln2-2a.(12分)
综上可知,当0<a<ln2时,最小值是-a;
当a≥ln2时,最小值是ln2-2a.(14分)

练习册系列答案
相关题目
 在区间
在区间 上的最小值是_________________;
上的最小值是_________________;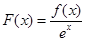 是定义在
是定义在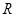 上的函数,其中
上的函数,其中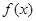 的导函数为
的导函数为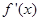 ,满足
,满足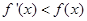 对于
对于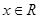 恒成立,则
恒成立,则



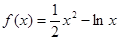 的单调递减区间为( )
的单调递减区间为( ) 1,1)
1,1)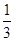 x3-
x3-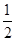 ax2+(a-1)x+1在区间(1,4)上是减函数,在区间(6,+∞)上是增函数,则实数a的取值范围是________.
ax2+(a-1)x+1在区间(1,4)上是减函数,在区间(6,+∞)上是增函数,则实数a的取值范围是________.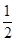 x2+blnx在区间[
x2+blnx在区间[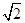 ,+∞)上是减函数,则b的取值范围是________.
,+∞)上是减函数,则b的取值范围是________.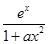 ,其中a为正实数.
,其中a为正实数.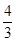 时,求f(x)的极值点;②若f(x)为R上的单调函数,求a的取值范围.
时,求f(x)的极值点;②若f(x)为R上的单调函数,求a的取值范围.