题目内容
设定义在R上的函数f(x)是最小正周期为2π的偶函数;f′(x)是f(x)的导函数,当x∈[0,π]时,0<f(x)<1;当x∈(0,π)且x≠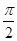 时,
时, f′(x)>0.则函数y=f(x)-sin x在[-2π,2π]上的零点个数为________.
f′(x)>0.则函数y=f(x)-sin x在[-2π,2π]上的零点个数为________.
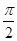 时,
时, f′(x)>0.则函数y=f(x)-sin x在[-2π,2π]上的零点个数为________.
f′(x)>0.则函数y=f(x)-sin x在[-2π,2π]上的零点个数为________.4
∵ f′(x)>0,x∈(0,π)且x≠
f′(x)>0,x∈(0,π)且x≠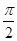 .
.
∴当0<x<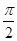 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在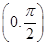 上递减.
上递减.
当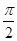 <x<π时,f′(x)>0,f(x)在
<x<π时,f′(x)>0,f(x)在 上递增.
上递增.
∵x∈[0,π]时,0<f(x)<1.∴当x∈[π,2π],则0≤2π-x≤π.
又f(x)是以2π为最小正周期的偶函数,
知f(2π-x)=f(x).∴x∈[π,2π]时,仍有0<f(x)<1.
依题意及y=f(x)与y=sin x的性质,在同一坐标系内作y=f(x)与y=sin x的简图.
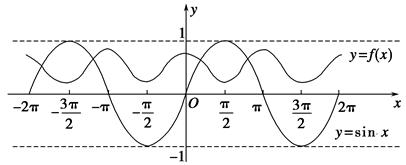
则y=f(x)与y=sin x,x∈[-2π,2π]有4个交点.
故函数y=f(x)-sin x在[-2π,2π]上有4个零点.
 f′(x)>0,x∈(0,π)且x≠
f′(x)>0,x∈(0,π)且x≠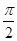 .
.∴当0<x<
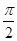 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在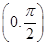 上递减.
上递减.当
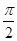 <x<π时,f′(x)>0,f(x)在
<x<π时,f′(x)>0,f(x)在 上递增.
上递增.∵x∈[0,π]时,0<f(x)<1.∴当x∈[π,2π],则0≤2π-x≤π.
又f(x)是以2π为最小正周期的偶函数,
知f(2π-x)=f(x).∴x∈[π,2π]时,仍有0<f(x)<1.
依题意及y=f(x)与y=sin x的性质,在同一坐标系内作y=f(x)与y=sin x的简图.

则y=f(x)与y=sin x,x∈[-2π,2π]有4个交点.
故函数y=f(x)-sin x在[-2π,2π]上有4个零点.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
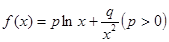 ,若
,若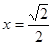 时,
时,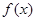 有极小值
有极小值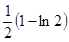 ,
,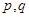 的取值;
的取值;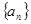 中,
中,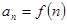 ,求证:数列
,求证:数列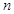 项和
项和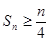 ;
;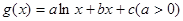 ,若
,若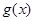 有极值且极值为
有极值且极值为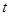 ,则
,则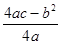 是否具有确定的大小关系?证明你的结论.
是否具有确定的大小关系?证明你的结论.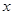 元/本(9≤
元/本(9≤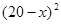 万本.
万本.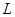 (万元)与每本书的定价
(万元)与每本书的定价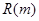 .
.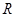 上的函数
上的函数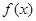 ,其导函数
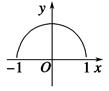
,其导函数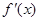 的图像如图所示,则下列叙述正确的是( )
的图像如图所示,则下列叙述正确的是( )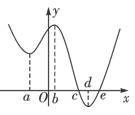
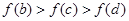
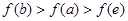
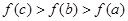

 x2-ln x的单调递减区间为 ( ).
x2-ln x的单调递减区间为 ( ).  的单调递增区间为( )
的单调递增区间为( )  和
和


